PS Azimuth Moveout

Azimuth moveout for converted waves (PS-AMO) is especially designed to process PS data, since it handles the asymmetry of the raypaths. PS-AMO moves events across a common reflection point according to their geological dips Rosales and Biondi (2006).

Theoretically, the cascade of any imaging operator with its corresponding forward-modeling operator generates a partial-prestack operator Biondi et al. (1998). A cascade operation of PS-DMO and its inverse (PS-DMO^-1) is the basic procedure that I follow to derive the PS-AMO operator. First, I present a Kirchhoff integral derivation of the PS-AMO operator using a 3-D extension of the 2-D PS-DMO operator.

Following the derivation of the AMO operator Biondi et al. (1998), I collapse the PS-DMO operator with its inverse. Figure  schematically illustrates the PS-AMO transformation. The axes are the x and y CMP coordinates. Figure  shows four important vectors. The vectors $\bf D_{10}$ and $\bf D_{02}$ are transformation vectors, extensions of the offset vectors $\bf h_1$ and $\bf h_2$ respectively, according to the equations that will follow. These transformation vectors ($\bf D_{10}$ and $\bf D_{02}$) are responsible for the lateral shift needed for transforming a trace from the CMP domain into the CRP domain and vice versa. Figure  shows the surface representation of a trace with input offset vector $\bf h_1$, reflection point at the origin, and azimuth $\theta_1$. This trace is 1) translated to its corresponding CRP position using the transformation vector $\bf D_{10}$; 2) transformed into zero offset ($\bf x_0$) by a time shift with the PS-DMO operator (an intermediate step); 3) converted into equivalent data in the CRP domain with; and finally, 4) translated to its corresponding CMP position, using the transformation vector $\bf D_{02}$, with output offset vector $\bf h_2$, midpoint $\bf x$, and azimuth $\theta_2$.

 

plane_new
Figure 1 Schematic of the PS-AMO transformation. An input trace with offset vector $\bf h_1$ and reflection point at the origin is transformed into equivalent data with offset vector $\bf h_2$ and midpoint position $\bf x$ after a transformation in and out of the CRP domain with the transformation vectors $\bf D_{10}=qp$ and $\bf D_{02}=tr$.

Appendix D presents the derivation of the PS-AMO operator, which is as follows:

 

$$t_2^2=t_1^2 \frac{\Vert{\bf h_{2}}\Vert^2}{\Vert{\bf h_{1}}\... ...{x}}\Vert^2\sin^2(\theta_1 - \Delta\phi) - {B_2}} \right \},$$ (35)

where

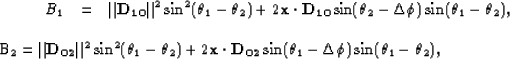$$\begin{eqnarray} {B_1}& = & \Vert{\bf D_{10}}\Vert^2\sin^2(\theta_1 - \theta_2)... ...f D_{02}}\sin(\theta_1 - \Delta\phi)\sin(\theta_1 - \theta_2), \end{eqnarray}$$ (36) (37)

and

$$\begin{eqnarray} {\bf D_{10}}&=&\left[ 1 + \frac{4\gamma \Vert {\bf h_1}\Vert ^2... ... {\bf h_2} \Vert^2}\right] \frac{1-\gamma}{1+\gamma} {\bf h_2}. \end{eqnarray}$$ (38) (39)

Equation , combined with equations -to-, represents an asymmetrical saddle on the CMP coordinates (x_x,x_y). In these equations, t₁ is the input time after PS-NMO, t₂ is the time after PS-AMO and before inverse PS-NMO, $\bf h_1$ and $\bf h_2$ are the input and output offset vectors, respectively, $\alpha$ is a scaling factor ($\alpha = 2\sqrt{\gamma}/(1+\gamma)$), $\gamma$ is the P-to-S velocity ratio, $\theta_1$ and $\theta_2$ are the input and output azimuth positions, respectively, B₁ and B₂ are the scalar quantities that relate the transformation vectors, $\bf D_{10}$ and $\bf D_{02}$, with the final position ($\bf x$) for the input trace, and $\bf x$ is the final CMP trace position. Similarly, $\bf D_{10}$ is the transformation vector from the original trace position to the intermediate zero-offset position, and $\bf D_{02}$ is the transformation vector from the intermediate zero-offset position to the final trace position.

The PS-AMO operator transforms the input trace, with offset vector $\bf h_1$ and reflection point at the origin, into an equivalent trace with offset vector $\bf h_2$ and a reflection point shifted by the vector ${\bf x}=x(\cos\Delta\phi, \sin\Delta\phi)$, as shown in Figure .

The PS-AMO operator depends on the P-to-S velocity ratio ($\gamma$). Equation depends on the transformation vectors ($\bf D_{10}$ and $\bf D_{02}$), and the transformation vectors depend on the traveltime after normal moveout (t₁), the P velocity (v_p), and $\gamma$. Therefore, PS-AMO presents a non-linear dependency on the traveltime after normal moveout (t₁), the P velocity and $\gamma$. Because of this, PS-AMO varies with respect to traveltime even in constant-velocity media.

It is important to note that for a value of $\gamma=1$, both transformation vectors $\bf D_{10}$ and $\bf D_{02}$ become zero, and equation reduces to the known expression for AMO. Also, the PS-DMO operator, used in this section, assumes constant velocity; therefore, the PS-AMO operator of equation is based on a constant velocity assumption. Next, we discuss a computationally efficient implementation of the PS-AMO operator in the frequency-wavenumber log-stretch domain.

 

• f-k log-stretch PS-AMO
• Impulse response