




Next: Abandoned strategy for attenuating
Up: ELIMINATING NOISE AND SHIP
Previous: Preconditioning for accelerated convergence
Spikes and erratic noise glitches can be suppressed
with an approximate 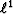 norm.
One main problem with the Galilee data is the presence of outliers
in the middle of the lake and at the track ends.
We could attenuate these spikes by editing or applying running median filters.
However, the former involves human labor
while the latter might compromise small details
by smoothing and flattening the signal.
Here we formulate the estimation
to eliminate the drastic effect of the noise spikes.
We introduce a weighting operator that deemphasizes high residuals as follows:
norm.
One main problem with the Galilee data is the presence of outliers
in the middle of the lake and at the track ends.
We could attenuate these spikes by editing or applying running median filters.
However, the former involves human labor
while the latter might compromise small details
by smoothing and flattening the signal.
Here we formulate the estimation
to eliminate the drastic effect of the noise spikes.
We introduce a weighting operator that deemphasizes high residuals as follows:
| 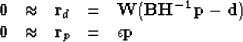 |
(23) |
with a diagonal matrix 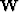 :
:
| 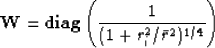 |
(24) |
where ri is the residual for one component of 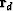 and
and 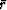 is a prechosen constant. This weighting operator
ranges from
is a prechosen constant. This weighting operator
ranges from 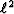 to
to 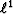 , depending on the constant
, depending on the constant 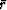 .We take
.We take 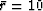 cm
because the data was given to us as integer multiples of 10 cm.
(A somewhat larger value might be more appropriate).
antoine2
cm
because the data was given to us as integer multiples of 10 cm.
(A somewhat larger value might be more appropriate).
antoine2
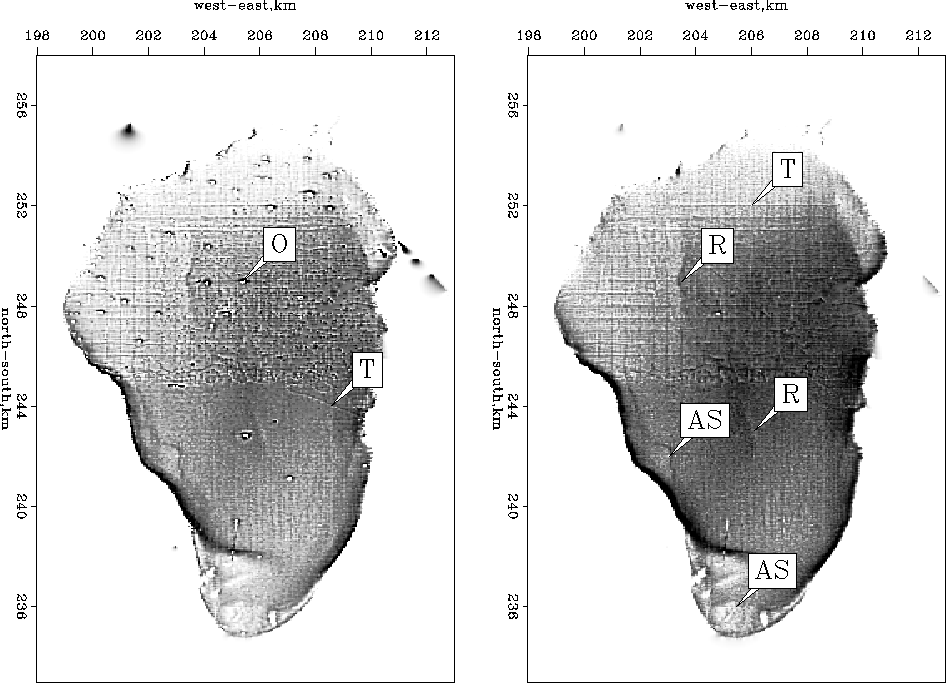
Figure 18 Estimated 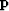 in a least-squares sense (left) and in an
in a least-squares sense (left) and in an
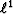 sense (right).
Pleasingly, isolated spikes are attenuated.
Some interesting features are shown by the arrows:
AS points to few ancient shores,
O points to some outliers,
T points to few tracks,
and R points to a curious feature.
sense (right).
Pleasingly, isolated spikes are attenuated.
Some interesting features are shown by the arrows:
AS points to few ancient shores,
O points to some outliers,
T points to few tracks,
and R points to a curious feature.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) displays
displays 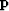 estimated
in a least-squares sense on the left and in a
estimated
in a least-squares sense on the left and in a 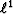 sense on the right
(equation (23) with a small
sense on the right
(equation (23) with a small 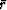 ).
Most of the glitches are no longer visible.
One obvious glitch remains near (x,y)=(205,238).
Evidently a north-south track has a long sequence of biased measurements
that our
).
Most of the glitches are no longer visible.
One obvious glitch remains near (x,y)=(205,238).
Evidently a north-south track has a long sequence of biased measurements
that our 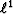 cannot overcome.
Some ancient shorelines in the western and southern parts of the Sea of
Galilee are now easier to identify (shown as AS).
We also start to see a valley in the middle of the lake (shown as R).
Data outside the lake (navigation errors) have been mostly removed.
Data acquisition tracks (mostly north-south lines and east-west lines,
one of which is marked with a T)
are even more visible after the suppression of the outliers.
cannot overcome.
Some ancient shorelines in the western and southern parts of the Sea of
Galilee are now easier to identify (shown as AS).
We also start to see a valley in the middle of the lake (shown as R).
Data outside the lake (navigation errors) have been mostly removed.
Data acquisition tracks (mostly north-south lines and east-west lines,
one of which is marked with a T)
are even more visible after the suppression of the outliers.
antoine3
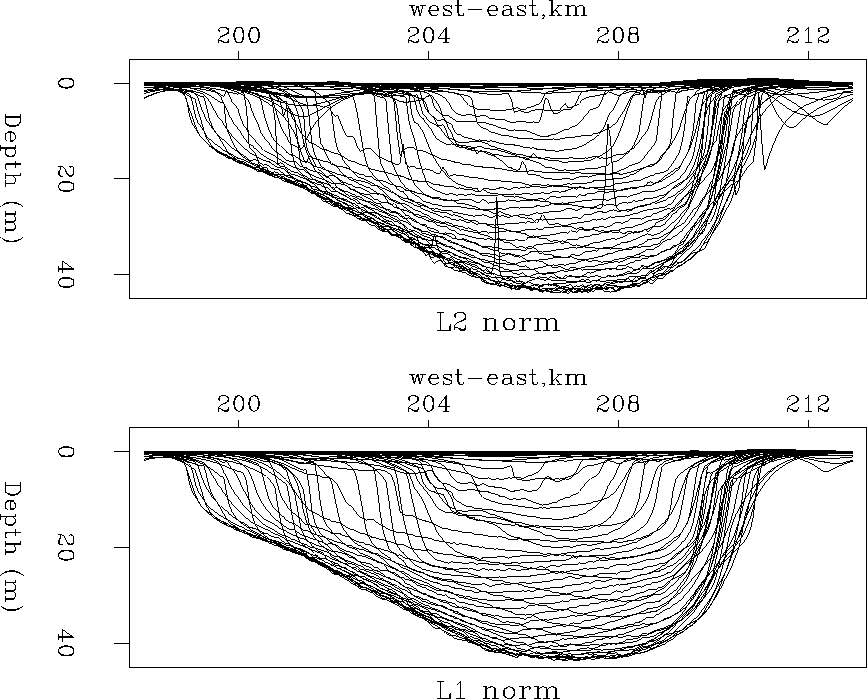
Figure 19
East-west cross sections of the lake bottom
( ).
Top with the
).
Top with the 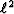 solution.
Bottom with the
solution.
Bottom with the 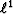 approximating procedure.
approximating procedure.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the bottom of the Sea of Galilee (
shows the bottom of the Sea of Galilee ( )with
)with 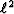 (top) fitting and
(top) fitting and 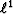 (bottom) fitting.
Each line represents one east-west transect,
transects at half-kilometer intervals on the north-south axis.
The
(bottom) fitting.
Each line represents one east-west transect,
transects at half-kilometer intervals on the north-south axis.
The 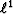 result is a nice improvement over the
result is a nice improvement over the 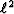 maps.
The glitches inside and outside the lake have mostly disappeared.
Also, the
maps.
The glitches inside and outside the lake have mostly disappeared.
Also, the 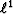 norm gives positive depths everywhere.
Although not visible everywhere in all the figures,
topography is produced outside the lake.
Indeed, the effect of regularization is to produce synthetic topography,
a natural continuation of the lake floor surface.
norm gives positive depths everywhere.
Although not visible everywhere in all the figures,
topography is produced outside the lake.
Indeed, the effect of regularization is to produce synthetic topography,
a natural continuation of the lake floor surface.
We are now halfway to a noise-free image.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that
vessel tracks overwhelm possible fine scale details.
Next we investigate a strategy based on the idea that
the inconsistency between tracks comes mainly
from different human and seasonal conditions during the data acquisition.
Since we have no records of the weather and the time
of the year the data were acquired
we presume that the depth differences between different acquisition tracks
must be small and relatively smooth along the super track.
shows that
vessel tracks overwhelm possible fine scale details.
Next we investigate a strategy based on the idea that
the inconsistency between tracks comes mainly
from different human and seasonal conditions during the data acquisition.
Since we have no records of the weather and the time
of the year the data were acquired
we presume that the depth differences between different acquisition tracks
must be small and relatively smooth along the super track.





Next: Abandoned strategy for attenuating
Up: ELIMINATING NOISE AND SHIP
Previous: Preconditioning for accelerated convergence
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) displays
displays ![]() estimated
in a least-squares sense on the left and in a
estimated
in a least-squares sense on the left and in a ![]() sense on the right
(equation (23) with a small
sense on the right
(equation (23) with a small ![]() ).
Most of the glitches are no longer visible.
One obvious glitch remains near (x,y)=(205,238).
Evidently a north-south track has a long sequence of biased measurements
that our
).
Most of the glitches are no longer visible.
One obvious glitch remains near (x,y)=(205,238).
Evidently a north-south track has a long sequence of biased measurements
that our ![]() cannot overcome.
Some ancient shorelines in the western and southern parts of the Sea of
Galilee are now easier to identify (shown as AS).
We also start to see a valley in the middle of the lake (shown as R).
Data outside the lake (navigation errors) have been mostly removed.
Data acquisition tracks (mostly north-south lines and east-west lines,
one of which is marked with a T)
are even more visible after the suppression of the outliers.
cannot overcome.
Some ancient shorelines in the western and southern parts of the Sea of
Galilee are now easier to identify (shown as AS).
We also start to see a valley in the middle of the lake (shown as R).
Data outside the lake (navigation errors) have been mostly removed.
Data acquisition tracks (mostly north-south lines and east-west lines,
one of which is marked with a T)
are even more visible after the suppression of the outliers.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the bottom of the Sea of Galilee (
shows the bottom of the Sea of Galilee (![]() )with
)with ![]() (top) fitting and
(top) fitting and ![]() (bottom) fitting.
Each line represents one east-west transect,
transects at half-kilometer intervals on the north-south axis.
The
(bottom) fitting.
Each line represents one east-west transect,
transects at half-kilometer intervals on the north-south axis.
The ![]() result is a nice improvement over the
result is a nice improvement over the ![]() maps.
The glitches inside and outside the lake have mostly disappeared.
Also, the
maps.
The glitches inside and outside the lake have mostly disappeared.
Also, the ![]() norm gives positive depths everywhere.
Although not visible everywhere in all the figures,
topography is produced outside the lake.
Indeed, the effect of regularization is to produce synthetic topography,
a natural continuation of the lake floor surface.
norm gives positive depths everywhere.
Although not visible everywhere in all the figures,
topography is produced outside the lake.
Indeed, the effect of regularization is to produce synthetic topography,
a natural continuation of the lake floor surface.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that
vessel tracks overwhelm possible fine scale details.
Next we investigate a strategy based on the idea that
the inconsistency between tracks comes mainly
from different human and seasonal conditions during the data acquisition.
Since we have no records of the weather and the time
of the year the data were acquired
we presume that the depth differences between different acquisition tracks
must be small and relatively smooth along the super track.
shows that
vessel tracks overwhelm possible fine scale details.
Next we investigate a strategy based on the idea that
the inconsistency between tracks comes mainly
from different human and seasonal conditions during the data acquisition.
Since we have no records of the weather and the time
of the year the data were acquired
we presume that the depth differences between different acquisition tracks
must be small and relatively smooth along the super track.