




Next: Importance of scaling
Up: PRECONDITIONING THE REGULARIZATION
Previous: PRECONDITIONING THE REGULARIZATION
The second miracle of conjugate gradients is exhibited below.
The data and data fitting matrix are the same,
but the model damping is simplified.
d(m) F(m,n) iter Norm
--- ------------------------------------------------ ---- ----------
41. -55. -90. -24. -13. -73. 61. -27. -19. 23. -55. 1 3.64410686
33. 8. -86. 72. 87. -41. -3. -29. 29. -66. 50. 2 0.31269890
-58. 84. -49. 80. 44. -52. -51. 8. 86. 77. 50. 3 -0.00000021
0. 100. 0. 0. 0. 0. 0. 0. 0. 0. 0. 4 -0.00000066
0. 0. 100. 0. 0. 0. 0. 0. 0. 0. 0. 5 -0.00000080
0. 0. 0. 100. 0. 0. 0. 0. 0. 0. 0. 6 -0.00000065
0. 0. 0. 0. 100. 0. 0. 0. 0. 0. 0. 7 -0.00000088
0. 0. 0. 0. 0. 100. 0. 0. 0. 0. 0. 8 -0.00000074
0. 0. 0. 0. 0. 0. 100. 0. 0. 0. 0. 9 -0.00000035
0. 0. 0. 0. 0. 0. 0. 100. 0. 0. 0. 10 -0.00000037
0. 0. 0. 0. 0. 0. 0. 0. 100. 0. 0. 11 -0.00000018
0. 0. 0. 0. 0. 0. 0. 0. 0. 100. 0. 12 0.00000000
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 100. 13 0.00000000
Even though the matrix is full-rank,
we see the residual drop about 6 decimal places after the third iteration!
This convergence behavior is well known
in the computational mathematics literature.
Despite its practical importance,
it doesn't seem to have a name or identified discoverer.
So I call it the ``second miracle.''
Practitioners usually don't like
the identity operator for model-shaping.
Generally they prefer to penalize wiggliness.
For practitioners,
the lesson of the second miracle of conjugate gradients
is that we have a choice of many iterations,
or learning to transform
independent variables so that
the regularization operator becomes an identity matrix.
Basically, such a transformation reduces the iteration count
from something about the size of the model space
to something about the size of the data space.
Such a transformation is called preconditioning.
In practice, data is often accumulated in bins.
Then the iteration count is reduced (in principle)
to the count of full bins
and should be independent of the count of the empty bins.
This allows refining the bins, enhancing the resolution.
More generally,
the model goal 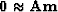 introduces a roughening operator like a gradient,
Laplacian
(and in chapter
introduces a roughening operator like a gradient,
Laplacian
(and in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a Prediction-Error Filter (PEF)).
Thus the model goal is usually a filter,
unlike the data-fitting goal
which involves all manner of geometry and physics.
When the model goal is a filter its inverse is also a filter.
Of course this includes multidimensional filters with a helix.
a Prediction-Error Filter (PEF)).
Thus the model goal is usually a filter,
unlike the data-fitting goal
which involves all manner of geometry and physics.
When the model goal is a filter its inverse is also a filter.
Of course this includes multidimensional filters with a helix.
The preconditioning transformation
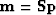 gives us
gives us
| 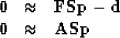 |
(6) |
The operator 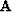 is a roughener while
is a roughener while 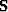 is a smoother.
The choices of both
is a smoother.
The choices of both 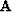 and
and 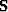 are somewhat subjective.
This suggests that we eliminate
are somewhat subjective.
This suggests that we eliminate 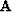 altogether
by defining it to be proportional to the inverse of
altogether
by defining it to be proportional to the inverse of 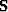 ,thus
,thus 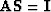 .The fitting goals become
.The fitting goals become
| 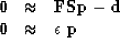 |
(7) |
which enables us to benefit from the ``second miracle''.
After finding 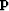 ,we obtain the final model with
,we obtain the final model with 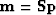 .
.





Next: Importance of scaling
Up: PRECONDITIONING THE REGULARIZATION
Previous: PRECONDITIONING THE REGULARIZATION
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a Prediction-Error Filter (PEF)).
Thus the model goal is usually a filter,
unlike the data-fitting goal
which involves all manner of geometry and physics.
When the model goal is a filter its inverse is also a filter.
Of course this includes multidimensional filters with a helix.
a Prediction-Error Filter (PEF)).
Thus the model goal is usually a filter,
unlike the data-fitting goal
which involves all manner of geometry and physics.
When the model goal is a filter its inverse is also a filter.
Of course this includes multidimensional filters with a helix.