




Next: Fourier transforms in retarded
Up: RETARDED COORDINATES
Previous: Definition of dependent variables
The familiar partial-differential equations of
physics come to us in (t,x,z)-space.
The chain rule for partial differentiation will
convert the partial derivatives
to (t' ,x' ,z' )-space.
For example, differentiating (30) with respect to z gives
| 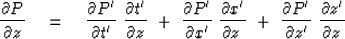 |
(31) |
Using (27), (28) and (29) to evaluate the
coordinate derivatives gives
| 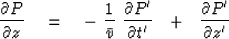 |
(32) |
There is nothing special about the variable P in (31)
and (32).
We could as well write
| 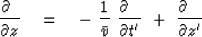 |
(33) |
where the left side is for operation on
functions that depend on (t,x,z) and the right
side is for functions of (t' ,x' ,z' ).
Differentiating twice gives
| 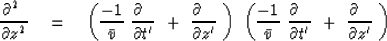 |
(34) |
Using the fact that the velocity is always time-independent results in
| 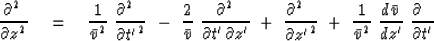 |
(35) |
Except for the rightmost term with the square brackets it could be said that
``squaring'' the operator (33) gives the second derivative.
This last term is almost always neglected in data processing.
The reason is that its effect is similar
to the effect of other first-derivative
terms with material gradients for coefficients.
Such terms,
cause amplitudes
to be more carefully computed.
that all such terms should be included, from the beginning.





Next: Fourier transforms in retarded
Up: RETARDED COORDINATES
Previous: Definition of dependent variables
Stanford Exploration Project
10/31/1997