Next: The (z,t)-plane method
Up: STACKING AND VELOCITY ANALYSIS
Previous: Lateral interpolation and extrapolation
Summing a common-midpoint gather on a hyperbolic trajectory over offset
yields a stack called a
constant-velocity
or a
CV
stack.
A velocity space may be defined as a family of CV stacks,
one stack for each of many velocities.
CV stacking is a transformation from
offset
space to
velocity
space.
CV stacking creates a (t,v)-space velocity panel
from a (t,h)-space common-midpoint gather.
Conventional industrial velocity estimation
amounts to CV stacking supplemented by squaring and normalizing.
Linear transformations such as CV stack are generally
invertible,
but the transformation to velocity space is of very high dimension.
Forty-eight channels and 1000 time points make
the transformation 48,000-dimensional.
With present computer technology,
matrices this large cannot be inverted by algebraic means.
However, there are some excellent approximate means of inversion.
For unitary matrices, the transpose matrix equals the inverse matrix.
In wave-propagation theory, a
transpose
operator is often a good approximation to an
inverse
operator.
Thorson [1984] pointed out
that the transpose operation to CV stacking is
just about the same thing as CV stacking itself.
To do the operation transposed to CV stacking,
begin with a velocity panel, that is, a panel in (t,v)-space.
To create some given offset h,
each trace in the (t,v)-panel must be first compressed to undo the
original NMO stretch.
That is, events must be pushed from the zero-offset time
that they have in the (t,v)-panel to the time appropriate for the given h.
Then stack the (t,v)-panel over v to produce the
seismogram for the given h.
Repeat the process for all desired values of h.
The program for transpose CV stack is like the program
for CV stack itself, except that the stretch formula
is changed to a compensating compression.
The inversion of a CV stack is analogous
to inversion of slant stack or Radon transformation.
That is,
the CV stack is almost its own inverse,
but you need to change a sign, and at the end,
a filtering operation, like rho filtering,
is also needed to touch up the spectrum, thereby finishing the job.
It is the rho filtering that distinguishes
inverse
CV stack
from the
transpose
of CV stack.
The word
transpose
refers to
matrix
transpose.
It is difficult to visualize why the word transpose is appropriate
in this case because we are discussing data spaces that are two-dimensional
and operators that are four-dimensional.
But if you will map these two- and four-dimensional objects
to familiar one- and two-dimensional objects
by a transformation
then you will see that
the word
transpose
is entirely appropriate.
The rho-type filtering required for CV stacks is slightly more complicated
than ordinary rho filtering--refer to Thorson [1984].
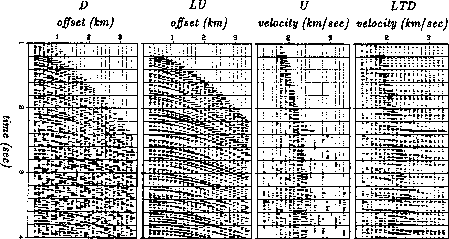
Figure 7 shows an example of Thorson's velocity space inversion.
Panel D is the original common-midpoint gather.
thor
Figure 7
Panel D at the left is a CMP gather from the Gulf of Mexico
(Western Geophysical).
The second panel (LU) is reconstructed data
obtained from the third panel (U)
by inverse NMO and stack.
The last panel (LTD) is a CV stack of the first panel. (Thorson)

Next is panel LU, the approximate reconstruction of D from velocity space.
The hyperbolic events are reconstructed much better than the random noise.
The random noise was not reconstructed so well because
the range of velocities in the CV stack was limited between water velocity
and 3.5 km/sec.
The next two panels (U) and (LTD) are theoretically related by
the ``rho'' filtering.
LTD is the CV stack of D.
LU is the transpose CV stack of U.
It is worth noting that there is a substantial amount of work
in computing a velocity panel.
A stack must be computed for each velocity.
Velocity discrimination by
wave-equation methods will be described next.
The wave-equation methods are generally cheaper,
though not fully comparable in effect.





Next: The (z,t)-plane method
Up: STACKING AND VELOCITY ANALYSIS
Previous: Lateral interpolation and extrapolation
Stanford Exploration Project
10/31/1997