




Next: Time domain versus frequency
Up: MULTIVARIATE LEAST SQUARES
Previous: Normal equations
Complex numbers frequently arise in physical problems,
particularly with Fourier series.
Let us extend the multivariable least-squares theory
to the use of complex-valued unknowns  .First recall how complex numbers were handled
with single-variable least squares,
i.e., as in the discussion leading up to equation (
.First recall how complex numbers were handled
with single-variable least squares,
i.e., as in the discussion leading up to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Use prime, such as
).
Use prime, such as 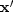 , to denote the complex conjugate
of the transposed vector
, to denote the complex conjugate
of the transposed vector  .Now write the positive quadratic form as
.Now write the positive quadratic form as
| 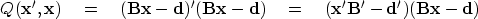 |
(25) |
In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (after equation (
(after equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )),
we minimized a quadratic form
)),
we minimized a quadratic form 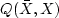 by setting to zero both
by setting to zero both
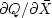 and
and 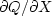 .We noted that only one of
.We noted that only one of
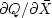 and
and 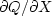 is necessary
because they are conjugates of each other.
Now take the derivative of Q
with respect to the (possibly complex, row) vector
is necessary
because they are conjugates of each other.
Now take the derivative of Q
with respect to the (possibly complex, row) vector 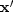 .Notice that
.Notice that 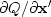 is the complex conjugate transpose
of
is the complex conjugate transpose
of 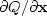 .Thus, setting one to zero sets the other also to zero.
Setting
.Thus, setting one to zero sets the other also to zero.
Setting 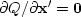 gives the normal equations:
gives the normal equations:
| 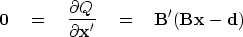 |
(26) |
The result is merely the complex form of
our earlier result (14).
Therefore,
differentiating by a complex vector
is an abstract concept,
but it gives the same set of equations
as differentiating by each scalar component,
and it saves much clutter.





Next: Time domain versus frequency
Up: MULTIVARIATE LEAST SQUARES
Previous: Normal equations
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Use prime, such as
).
Use prime, such as ![]() .First recall how complex numbers were handled
with single-variable least squares,
i.e., as in the discussion leading up to equation (
.First recall how complex numbers were handled
with single-variable least squares,
i.e., as in the discussion leading up to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Use prime, such as
).
Use prime, such as ![]() , to denote the complex conjugate
of the transposed vector
, to denote the complex conjugate
of the transposed vector ![]() .Now write the positive quadratic form as
.Now write the positive quadratic form as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (after equation (
(after equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )),
we minimized a quadratic form
)),
we minimized a quadratic form