




Next: Mutes
Up: Symes: Differential semblance
Previous: The Convolutional Model for
As an approximate predictor of seismic traces, the
convolutional model exhibits several types of error:
- physics error: seismic waves are not small amplitude
pressure waves in a fluid;
- linearization error: neglect of multiple reflections and
other nonlinear effects;
- deconvolution error: complete removal of the source signature is not
possible;
- asymptotic error: the convolutional model becomes more accurate as
the frequency content of r(t0,x) moves away from zero Hz.
The practical meaning of asymptotic error is that the convolutional model
predicts the higher frequency components of the data more accurately, so
that the prediction error can be reduced by more aggressive
low-cut filtering. Of course this discarding of low-frequency data is only
possible to a limited extent as actual data is bandlimited.
The following computations will introduce yet more sources of
asymptotic error - and, with one exception, only asymptotic
error. Therefore I will identify asymptotic error explicitly, and
treat other types of modeling error as data noise. It is possible to
estimate every asymptotic error explicitly, but experience suggests
that these explicit estimates are not particularly useful. So instead
I will use the symbol ``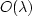 '' to suggest proportionality of
the asymptotic error to a dominant wavelength in the data. Thus
'' to suggest proportionality of
the asymptotic error to a dominant wavelength in the data. Thus
![\begin{displaymath}
F[v]r(t,x)=a(t,x)r(T_0(t,x),x) + O(\lambda)\end{displaymath}](img7.gif)
The single important lesson to learn from the explicit error estimates
of geometric optics is that they are uniform over 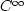 -bounded
sets of coefficients (meaning in this case the velocity v). Therefore
the velocities appearing in the sequel are restricted to vary over such a
-bounded
sets of coefficients (meaning in this case the velocity v). Therefore
the velocities appearing in the sequel are restricted to vary over such a
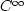 -bounded set. A byproduct of the analysis will suggest
explicit finite dimensional subspaces of smooth functions in which
it is advantageous to seek v.
-bounded set. A byproduct of the analysis will suggest
explicit finite dimensional subspaces of smooth functions in which
it is advantageous to seek v.





Next: Mutes
Up: Symes: Differential semblance
Previous: The Convolutional Model for
Stanford Exploration Project
4/20/1999
![]() '' to suggest proportionality of
the asymptotic error to a dominant wavelength in the data. Thus
'' to suggest proportionality of
the asymptotic error to a dominant wavelength in the data. Thus
![]()
![]() -bounded
sets of coefficients (meaning in this case the velocity v). Therefore
the velocities appearing in the sequel are restricted to vary over such a
-bounded
sets of coefficients (meaning in this case the velocity v). Therefore
the velocities appearing in the sequel are restricted to vary over such a
![]() -bounded set. A byproduct of the analysis will suggest
explicit finite dimensional subspaces of smooth functions in which
it is advantageous to seek v.
-bounded set. A byproduct of the analysis will suggest
explicit finite dimensional subspaces of smooth functions in which
it is advantageous to seek v.