DEVELOPMENT

In the normal incidence case of Backus averaging, the layer properties of thickness, $\Delta Z_{\jmath}$, compliance, $S_{\jmath}$, and mass density, $R_{\jmath}$, are replaced by the corresponding properties of the equivalent homogeneous medium, $Z_{\rm equiv}$, $S_{\rm equiv}$,and $R_{\rm equiv}$:

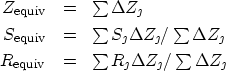$$\begin{eqnarray} Z_{\rm equiv} & = & \textstyle \sum\Delta Z_{\jmath} \\ S_{\rm... ...\sum R_{\jmath} \Delta Z_{\jmath}/\textstyle \sum\Delta Z_{\jmath}\end{eqnarray}$$ (1) (2) (3)

that is, the thickness of $Z_{\rm equiv}$ is the sum thickness of the layers, $Z = \textstyle \sum\Delta Z_{\jmath}$, and the equivalent medium mechanical properties are the thickness-weighted averages of those of the layered medium.

However, these layers can also be described in terms of the layer properties of one-way travel-time, $\Delta T_{\jmath}$, and impedance, $I_{\jmath}$, with slowness, $L_{\jmath}$ acting as the means for changing the independent variable between depth and time. It is well known that:

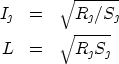$$\begin{eqnarray} I_{\jmath} & = & \sqrt{R_{\jmath}/S_{\jmath}} \\ L & = & \sqrt{R_{\jmath} S_{\jmath}}\end{eqnarray}$$ (4) (5)

and from these:

$$\begin{eqnarray} R_{\jmath} & = & I_{\jmath} L_{\jmath} \\ S_{\jmath} & = & I^{-1}_{\jmath} L_{\jmath}\end{eqnarray}$$ (6) (7)

and thus:

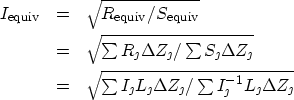$$\begin{eqnarray} I_{\rm equiv} & = & \sqrt{R_{\rm equiv}/S_{\rm equiv}} \nonumbe... ...ath}/\textstyle \sum I^{-1}_{\jmath} L_{\jmath} \Delta Z_{\jmath}}\end{eqnarray}$$ (8)

but $L_{\jmath} \Delta Z_{\jmath} = \Delta T_{\jmath}$, so:

$$I_{\rm equiv} = \sqrt{\textstyle \sum I_{\jmath} \Delta T_{\jmath}/\textstyle \sum I^{-1}_{\jmath} \Delta T_{\jmath}}$$ (9)

and by similar reasoning the slowness equivalent:

$$L_{\rm equiv} = (\textstyle \sum\Delta Z_{\jmath})^{-1}\sqrt... ...ta T_{\jmath}\textstyle \sum I^{-1}_{\jmath} \Delta T_{\jmath}}$$ (10)

and, since $T_{\rm equiv}$ = $Z_{\rm equiv}L_{\rm equiv}$:

$$T_{\rm equiv} = \sqrt{\textstyle \sum I_{\jmath} \Delta T_{\jmath}\textstyle \sum I^{-1}_{\jmath} \Delta T_{\jmath}}$$ (11)