More about IRLS

All the convergence issues discussed above are dramatically altered if I change the restart parameter, the weighting function, and the damping factor. This means we have to make many decisions about a single inverse problem. To illustrate even more clearly the complexity of IRLS algorithms, I below give a list of weighting functions I found in the literature ($\epsilon$ positive constant):

$$w_{ii}=\frac{1}{[1+(r_{ii}/\epsilon)^2]^{1/4}},$$

Bube and Langan (1997),

$$w_{ii}=\frac{2\bar{r}}{\vert r_{ii}\vert+r_{ii}},$$

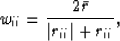
Fomel and Claerbout (1995),

$$w_{ii}= \left\{ \begin{array} {cc} \vert r_{ii}\vert^{(p-2)/... ...rt^{(p-2)/2}, & \vert r_{ii}\vert < \epsilon \end{array}\right.$$

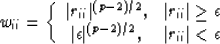
with p=1, Huber (1981),

$$w_{ii}=\frac{p^{1/2}}{(\vert r_{ii}\vert+\epsilon)^{(2-p)/2}},$$

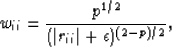
with p=1, Hugonnet (1998), and finally

$$w_{ii}=\frac{1}{\sqrt{1+(r_{ii}/\epsilon)^2}}.$$

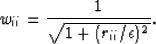
Claerbout and Fomel (1999), and there is probably more.

Each weighting function has different pros and cons and should be carefully chosen according to the problem we are trying to solve. Generally speaking, they all aim to weight down outliers in the data. With only the threshold to set up a priori, the Huber solver appears far easier to utilize than IRLS algorithms. Moreover, on a velocity stack inversion problem, for a very common weighting function (equation 5) with reasonable parameters (damping factor and restart parameter), I have shown that the Huber norm fosters better convergence than IRLS.