Next: Theorem
Up: Guitton: Huber solver
Previous: Introduction
This part follows closely Kelley 's Iterative Method for Optimization Kelley (1999).
We start here with a series of definitions:
- 1.
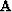 is positive definite if
is positive definite if 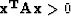 for all
for all 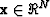
- 2.
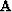 is spd if
is spd if 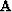 is positive definite and symmetric
is positive definite and symmetric
- 3.
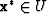 (
(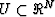 ) is a global minimizer if
) is a global minimizer if
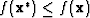 for all
for all 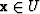
The Euclidian norm is also defined as
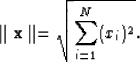
Now, I give sufficient conditions that a minimizer 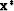 exists for a function f.
exists for a function f.





Next: Theorem
Up: Guitton: Huber solver
Previous: Introduction
Stanford Exploration Project
4/27/2000