Wave equation angle gathers

When doing velocity analysis, general practice is to measure moveout from a relatively sparse set of CRP gathers. Kirchhoff depth migration is the preferred construction method because it can produce the sparse set of CRP gathers without needing to image the entire volume. In addition, if our Green's function table is constructed correctly, Kirchhoff methods do not suffer from the velocity approximations needed by frequency domain methods. Kirchhoff methods also have some deficiencies. The most glaring weakness of Kirchhoff methods is the difficulty in constructing the Green's function table. To construct an accurate Green's function table we must account for, and weight correctly, the multiple arrivals that occur in complex geology. Calculating and accounting for multiple arrivals adds significantly to both coding complexity and memory requirements. As a result, a single arrival is often all that is used. Eikonal methods Fomel (1997); Podvin and Lecomte (1991); Vidale (1990); van Trier and Symes (1991) can efficiently produce first arrivals, but in areas of complex geology the first arrival is not always the most important arrival Audebert et al. (1997). Nichols (1994) proposed a band-limited method that gave the maximum amplitude arrival, but the method is computationally impractical in 3-D. As a result, people usually go to expensive ray based methods but still face the difficult tasks of choosing the most important arrival and correctly and efficiently interpolate the traveltime field Sava and Biondi (1997).

The most computationally attractive alternative to Kirchhoff methods is frequency domain downward continuation. Downward continuation has its own weaknesses. Its primary weakness is speed. Downward continuation can not be target oriented, so full volume imaging is required. In addition, frequency domains methods in their purest form can not handle lateral variations in velocity. By migrating with multiple velocities and applying a space domain correction to the wavefield, they can do a fairly good job handling lateral variations (this migration is normally referred to as PSPI, Phase-shift plus interpolation)Ristow and Ruhl (1993). Finally, downward continuation focuses the wavefield towards zero offset, making conventional moveout analysis impossible.

We can create CRP gathers where moveout analysis is possible by changing our imaging condition Clayton and Stolt (1981); Prucha et al. (1999). Given a wave-field we follow the normal procedure of downward continuing the data and extracting the image at the surface z=0 and zero time. Instead of extracting the image at zero offset, we note that reflection angle 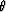$\theta$ can be evaluated by the differential equation:

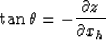$$\tan \theta = - \frac{\partial z}{\partial x_h}$$ (5)

where z is the depth, x_h is half-offset.

The topic of this paper is not migration, but tomography. The tomography method could be applied with either Kirchhoff or PSPI. For us, PSPI proved to be a more attractive choice. A 2-D and 3-D PSPI algorithm was already available, where a Kirchhoff approach would have required the coding of the migration algorithm along with a suitable traveltime computation method.