Median of an even number of points

Consider four numerical values, say (5,7,98,100). The median value is the middle value. Since this is an even number of points, there is no middle. A way to define the median m mathematically is to choose m to minimize

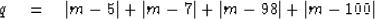$$q \quad =\quad\vert m-5\vert + \vert m-7\vert + \vert m-98\vert + \vert m-100\vert$$ (1)

If you plot the function q(m) you find it has a flat spot between m=7 and m=98. This illustrates a principle of L₁ optimizations: The minimum residual is unique. The model, however, is not unique, but is a range. This is an interesting feature of L₁ which differs from our usual least squares L₂ experience where we never get intervals. With L₂, solutions are unique, except for a possible null space, an infinite family of added solutions. Having a 5th data point, even if very weakly weighted, would resolve the ambiguity so we might be on the track of a Busch-like solution.