Let the layered earth response from shot s to geophone g
be u(s,g,t)=u(0,g-s,t)=u(g-s,t) or in Fourier space,
![]() or simply u(g-s).
When an upcoming wave hits the
earth surface at g1 it encounters a scattering object
which reflects the primary wave with a random scaling
or simply u(g-s).
When an upcoming wave hits the
earth surface at g1 it encounters a scattering object
which reflects the primary wave with a random scaling ![]() .The signal at g1 then takes off for a second flight
like a multiple reflection, but departing in all directions.
We are going to build the theoretical 2-D spectrum
of this surface scattered wave w from the theoretical 2-D spectrum of u,
the layered media primary reflection.
.The signal at g1 then takes off for a second flight
like a multiple reflection, but departing in all directions.
We are going to build the theoretical 2-D spectrum
of this surface scattered wave w from the theoretical 2-D spectrum of u,
the layered media primary reflection.
First we express the cascade of the two bounces. The arrival w
at g2 at time t is the sum of the time of each bounce,
![]() and
and ![]() .Since this is a convolution in the time domain,
we express it as a product in the frequency domain.
Then we form the complex conjugate of this expression in preparation for
autocorrelation on the x-axis.
.Since this is a convolution in the time domain,
we express it as a product in the frequency domain.
Then we form the complex conjugate of this expression in preparation for
autocorrelation on the x-axis.
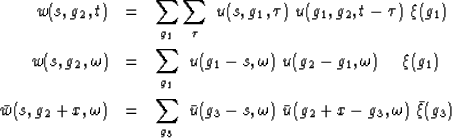 |
(1) | |
| (2) | ||
| (3) |
| (4) |
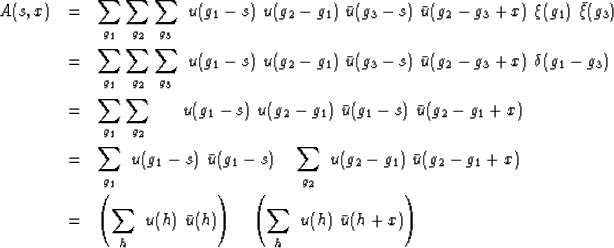 |
(5) | |
| (6) | ||
| (7) | ||
| (8) | ||
| (9) |
We Fourier transform over x.
The first factor above is not a function of space.
It is merely a function of ![]() , say a filter
, say a filter ![]() .Thus our main result:
.Thus our main result:
| (10) |
We see that in principle, for each shot point s, we measure the spectrum of the impulse response of the layered medium.