BURG PEF ESTIMATION REVIEW

Burg PEF estimation should work fine on a helix. Full details along with the 1-D code are found at Claerbout (1976). I will quickly review the theory from memory (partly to see how simple I can make it).

First is the notion that PEFs can be built up from this recursion

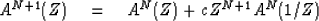$$A^{N+1}(Z) \quad =\quad A^{N}(Z) + c Z^{N+1} A^N(1/Z)$$ (1)

where c is in the range 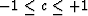$-1\le c\le+1$.There is a theorem from Algebra that is easy to prove that if c is in the required range, then A^N+1(Z) will be minimum phase if A^N(Z) is minimum phase. Since A⁰=1, all are minimum phase.

Burg's PEF calculation begins from two copies of the data X(Z). One, called F(Z) will be turned into the forward prediction error A(Z)X(Z). The other called B(Z) will be turned into the backward prediction error A(1/Z)X(Z). At each stage of the calculation, we compute c with this formula  

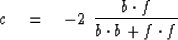$$c \quad =\quad- 2\ { b \cdot f \over b\cdot b + f\cdot f}$$ (2)

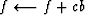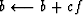The triangle inequality shows that for arbitrary f and b, c is in the required range. Given c we now form an upgraded F and B with $f\longleftarrow f+c b$ and $b\longleftarrow b+c f$.[At successive iterations, increasing time lag is introduced between f and b. Details in 1976.] When you are finished, you have F=A(Z)X(Z) and B=A(1/Z)X(Z). Why is that? To understand that requires delving into 1-D theory, in particular, the Levinson recursion, and we won't do that now. [Maybe I can think up an easier explanation later. Perhaps by a sequence of orthogonality arguments.] I recall if you append a tiny impulse function off the end of X before you start, when you finish, you will see it has turned into the PEF.

Now let us think about missing data off the ends of the Burgian one-dimensional data set. Given that we have computed F(Z)=A(Z)X(Z), then we should find that F(Z)/A(Z) matches X(Z) until its end, and it is a logical continuation thereafter. Likewise B(Z) could be used for extensions before the beginning of X(Z). Thus it remains to think about how to handle gaps in the middle.