




Next: About this document ...
Up: Vaillant & Biondi: Common-azimuth
Previous: REFERENCES
Here we derive the equation of circular rays in constant gradient
velocity media. Along a circular ray, the curvilinear abscissa s is,
with the previous notations:
| 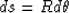 |
(13) |
The equations for the ray trajectory passing through points
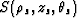 and
and 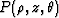 are
are
| 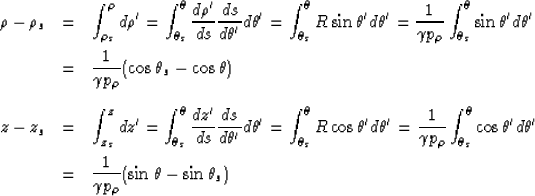 |
|
| (14) |
| |
| |
| (15) |
By writing the identity
| ![\begin{displaymath}
\cos^2 \theta + \sin^2 \theta =
\left[ \gamma p_\rho (\rho_...
...
\left[ - \gamma p_\rho (z_s - z) + \sin\theta_s \right]^2 = 1\end{displaymath}](img36.gif) |
(16) |
at every point along the ray, we obtain the equation of the desired circle:
| ![\begin{displaymath}
\left[ \rho - \rho_s - \frac{\cos \theta_s}{\gamma p_\rho} \...
...)}{\gamma} \right]^2 =
\left[ \frac{1}{\gamma p_\rho} \right]^2\end{displaymath}](img37.gif) |
(17) |





Next: About this document ...
Up: Vaillant & Biondi: Common-azimuth
Previous: REFERENCES
Stanford Exploration Project
4/28/2000
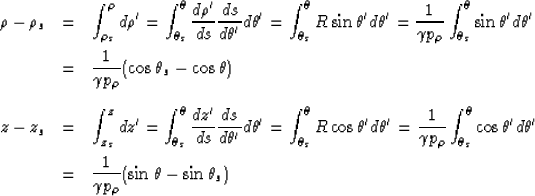
![\begin{displaymath}
\left[ \rho - \rho_s - \frac{\cos \theta_s}{\gamma p_\rho} \...
...)}{\gamma} \right]^2 =
\left[ \frac{1}{\gamma p_\rho} \right]^2\end{displaymath}](img37.gif)