Smoothing pixels versus smoothing micropatches

We can choose pixel-wise smoothing or micropatch smoothing. An easy argument favoring micropatches over pixel-wise smoothing says that putting a filter at every data sample is a tremendous waste of memory. If the data are predictable at all, they are probably not so nonstationary that they need a separate PEF at each sample. A single 3-D PEF has easily 20 or more adjustable coefficients, so allocating the set of PEFs requires 20 times the storage of the input data. Even very small micropatches require much less memory.

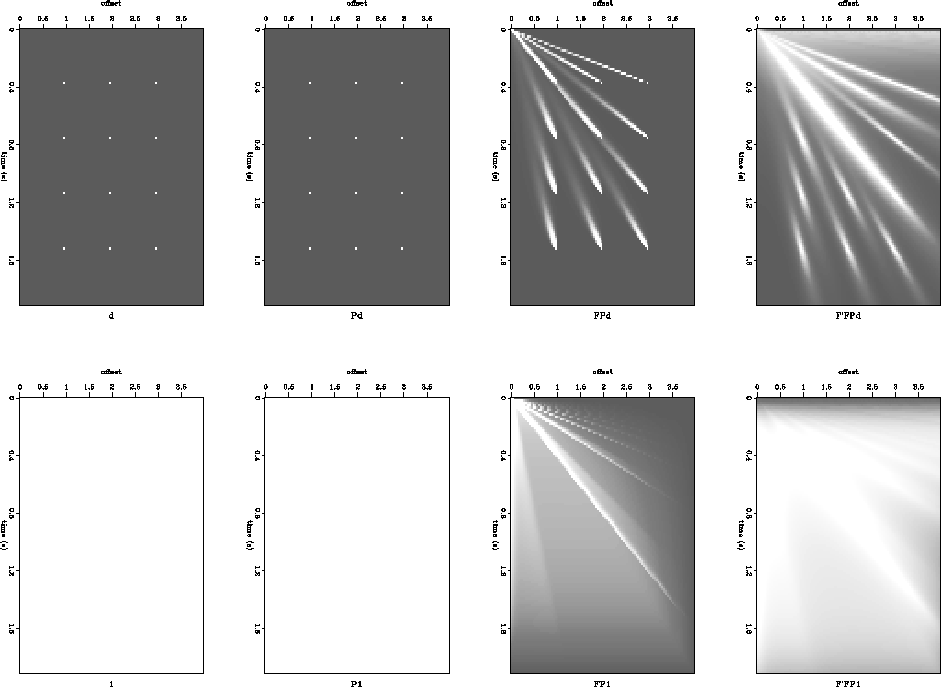
Micropatches also have some simplifying side effects that make them preferable to pixel-wise smoothing. One is apparent from examining Figures curtSmear8 and random8. Figure curtSmear8 shows smoothing in micropatches and Figure random8 shows pixel-wise smoothing. In each figure, the values represent filter coefficients displayed in data coordinates. The axes are time and offset. The top halves show a set of impulses, labeled $\bold d$.$\bold M \bold d$ is the impulses binned into micropatches, while $\bold P \bold d$ is the impulses binned into pixels (naturally, $\bold P \bold d = \bold d$). $\bold F$ and $\bold F'$ are pixel-wise smoothers pointed towards and away from zero radius, respectively. $\bold C$ and $\bold C'$ are the micropatched smoothers. In this case, the two are similar, though the pixel-wise smoother obviously produces a higher-resolution picture (though the micropatches could be made much smaller).

The bottom halves show the same treatment applied to a constant function, labeled $\bold 1$.$\bold M \bold 1$ has an angular limit applied. Pixel-wise smoothing creates some very large ridge artifacts, visible in $\bold F \bold P \bold 1$ and $\bold F' \bold F \bold P \bold 1$,where the angle between a data sample and the origin corresponds to an integer slope. Also, where the constant function is smoothed in towards zero radius, $\bold F \bold P \bold 1$, energy concentrates in a huge spike at the origin.

$\bold F'\bold F$ and $\bold C' \bold C$can be thought of as weighting functions in equation goodleak2 (either $\bold F'\bold F$ or $\bold C' \bold C$ is used for $\bold S$in that equation). It is desirable to have the flatter weighting function. It is also simpler to implement. Producing the many different angles in Figure random8 requires that the smoothers $\bold F$ and $\bold F'$ be made up of many different filters, oriented in a continuous sweep between a spatial derivative and a time derivative. $\bold C$ and $\bold C'$produce the same range of angles in Figure curtSmear8 using a single, radial derivative filter. The PEFs in micropatches are regularly gridded in angle and radius, so they are easily smoothed in those directions with old-fashioned stationary 1-D derivative filters. PEFs at every pixel are instead regularly sampled in time and offset, so working in polar coordinates requires some work. $\bold F$ uses many coefficients, $\bold C$ uses two.

 

curtSmear8
Figure 1 Illustration of micropatched radial filter coefficient smoothing.

 

random8
Figure 2 Illustration of pixel-wise radial filter coefficient smoothing.