2-D steering filter

In 2-D we build our steering filters by creating a series of dip annihilation filters that that destroy a given slope p_xz in a x-z plane. Further, we would like to control the bandwidth response of filters oriented at different slopes. We can achieve both these goals by constructing a triangle centered at the appropriate slope. Every grid cell center which the triangle passes through is assigned a negative value proportional to the height of the triangle at that location,

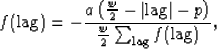$$f({\rm lag})=-\frac{a\left(\frac{w}{2}-\vert{\rm lag}\vert-p\right)}{\frac{w}{2} \sum_{{\rm lag}} f({\rm lag})} ,$$ (1)

where:

$f({\rm lag})$

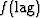
is the filter coefficient at a given lag (for lags where $f({\rm lag})<0$)

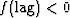a

is the amplitude of the filter (ranging from 0 to 1)

w

is the width of the triangle

p

is the slope.

The wider the triangle base, the less anisotropic our smoothing filter becomes. By increasing or decreasing a, we can increase or decrease the range over which the smoothing filter operates.