Next: Geometric interpretation
Up: geometric interpretation of the
Previous: Definitions
Following the preceding definitions, we can define the noise and
signal filters more precisely. But first, remind that
with
| 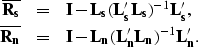 |
|
| (28) |
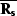 and
and 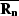 are signal and
noise filtering operators respectively. If we denote
are signal and
noise filtering operators respectively. If we denote
| 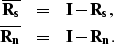 |
|
| (29) |
with 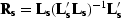 and
and
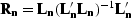 the signal and
noise resolution operators, we deduce that
the signal and
noise resolution operators, we deduce that 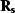 and
and 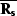 ,
, 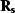 and
and 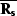 are
complementary operators (definition 2).
are
complementary operators (definition 2).
It can be shown that 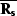 ,
, 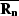 ,
,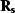 and
and 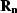 are projectors. For
are projectors. For 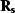 and
and 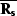 , we have
, we have
| 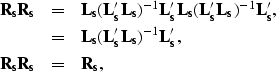 |
|
| |
| (30) |
and
| 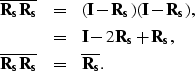 |
|
| |
| (31) |
Thus, 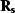 and
and 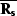 are projectors as defined
in definition 1. The same proofs work for
are projectors as defined
in definition 1. The same proofs work for 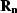 and
and 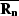 .
.
We can prove that 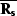 and
and 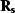 ,
, 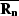 and
and 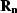 are mutually orthogonal. For
are mutually orthogonal. For 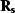 and
and 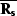 , we have
, we have
| 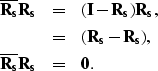 |
|
| |
| (32) |
Hence, 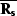 and
and 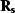 ,
, 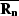 and
and 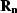 are complementary, mutually orthogonal projectors.
are complementary, mutually orthogonal projectors.





Next: Geometric interpretation
Up: geometric interpretation of the
Previous: Definitions
Stanford Exploration Project
4/29/2001
![]() ,
, ![]() ,
,![]() and
and ![]() are projectors. For
are projectors. For ![]() and
and ![]() , we have
, we have
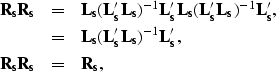
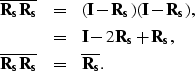
![]() and
and ![]() ,
, ![]() and
and ![]() are mutually orthogonal. For
are mutually orthogonal. For ![]() and
and ![]() , we have
, we have