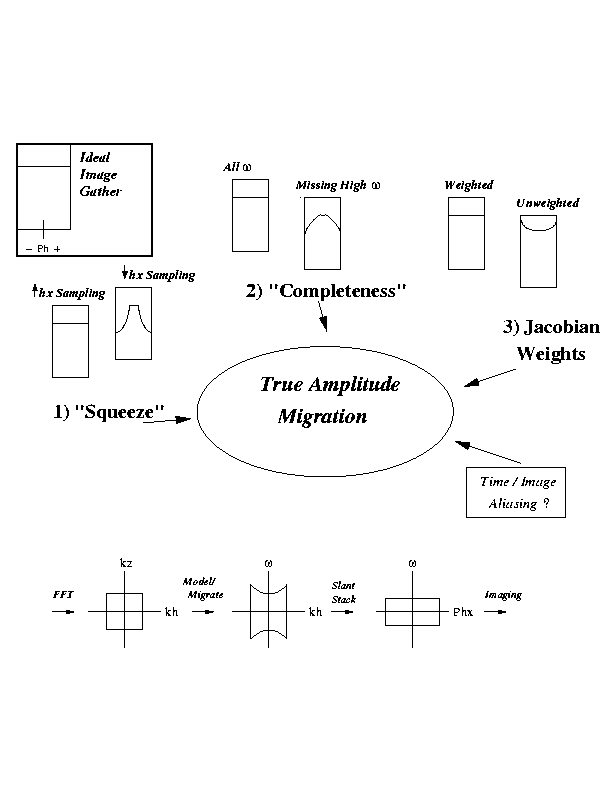
 |
Figure 1 Factors affecting amplitudes. The modeling/migration workflow is shown below.
When migrating seismic data for the purpose of reservoir characterization, it is necessary to use a migration algorithm that preserves relative amplitude trends Scheriff (1995). In the industry, this is usually attained using Kirchhoff methods with asymptotic Green's functions Biondi (2000). This method is useful in many geologic settings, but when a complex velocity Earth introduces more complex wave propagation phenomena, ``wave-equation'' migration (WEM) based on downward continuation becomes more attractive Prucha et al. (1999).
The goal of this paper is to address the problems associated with amplitude preservation encountered in WEM and how to correct them, at least to first order. Three effects will be discussed:
This paper shows that for relatively simple velocity models, a weight described by Sava and Biondi (2001) perfectly preserves amplitude trends. Also we outline a method to mute parts of an image gather outside the coverage of the recording geometry.
 |