Ratio of Compliance Differences

We have already seen that there are several advantages of the differential scheme presented here for purposes of analysis. Another advantage will soon become apparent when we analyze the ratio of the compliance differences

R = 1/G^* - 1/G_dry1/K^* - 1/K_dry.   This ratio is of both theoretical and practical interest. It is of practical interest because it is often easier to measure bulk moduli, and it would therefore be possible to estimate the shear behavior from the bulk behavior if the ratio R were known to be either a universal constant, or a predictable parameter. Mavko and Jizba (1991) show that this ratio is given by $R \simeq 4/15$ when the differences between the dry and the starred quantities are due to a small amount of soft (crack-like) porosity that is liquid filled for the starred moduli. The derivation of this ratio makes it clear that the value R = 4/15 is actually an upper bound, i.e., a value that cannot be exceeded for such systems, but also a value that clearly is not achieved for many systems lacking such soft porosity. In particular, it was already known by Mavko and Jizba (1991) that $R \simeq 0$ when the microgeometry of all the porosity is spherical. The crack-like porosity in Mavko and Jizba's model has finite compressiblity normal to its plane and is incompressible in the plane of the crack. Thus, their soft porosity can be thought of as cracks whose aspect ratios approach zero. Goertz and Knight (1998) have also done a parameter study showing that a related ratio (RG_m/K_m) is generally less than 4/15 for oblate spheroids and it tends to zero as the oblate spheroids' aspect ratios approach unity. It would be helpful to see this behavior directly in the equations, and it is the purpose of this section to show this behavior analytically.

Each of the four material constants appearing in (R) can be computed/estimated using the DEM. But, R is normally defined only in the limit of very small values of soft porosity, in which case both the numerator and the denominator tend to zero. This type of limit is well-known in elementary calculus, and the result is given by L'Hôpital's rule:

R = d(1/G^* - 1/G_dry)/dyd(1/K^* - 1/K_dry)/dy.   From this form of R, it is now quite easy to relate the ratio to the P's and Q's discussed earlier. In particular, we find that

(1-y)ddy(1/G^* - 1/G_dry) = 2K_f5G_m _m- 2G_m/3_m(K_f+_m)   and

(1-y)ddy(1/K^* - 1/K_dry) = - K_f_m(K_f+_m) (1 + 3(1-2_m)/4(1-_m^2)),   and therefore that

R = 415(1 - 34(1-_m)) (1 + 3(1-2_m)/4(1-_m^2))^-1.   [For sandstones, we could instead evaluate (R3) at $y = \phi_0$and $\nu(\phi_0) = \nu_s$. It is only the soft, crack-like porosity that needs to be very small for (R3) to be applicable.] Equation (R3) is an exact expression for the ratios of these two slopes when the calculation starts at y=0 and $\nu(0) = \nu_m$. It depends only on the aspect ratio $\alpha$ and Poisson's ratio $\nu_m$ of the mineral. It shows a sublinear decrease of R with increasing $\alpha$, and the value of R reaches zero when $\alpha_c = 4(1-\nu_m)/3\pi$. Because the formulas used for the penny-shaped crack model are valid only for very low aspect ratios, this latter behavior should not be taken literally. We do expect R to decrease as the aspect ratio increases, and the trend should be to zero, but this zero value should only be achieved at $\alpha = 1$.This is the type of behavior observed, for example, by Goertz and Knight (1998). We will check the quantitative predictions by doing a numerical study here for oblate spheroids as a function of aspect ratio. The results will be similar to those obtained by Goertz and Knight (1998), but not identical for several reasons: (1) Goertz and Knight plot RG_m/K_m (instead of R) for the Mori-Tanaka method (Benveniste, 1987), (2) the R values presented here are for an infinitesimal change in soft porosity, and (3) the present calculation is (therefore) actually not dependent on the type of effecive medium approximation used, only on the Eshelby (1957) and Wu (1966) factors P and Q.

 

Rratio_log
Figure 7 Ratio of compliance differences R as a function of aspect ratio for oblate spheroids and for the penny-shaped crack approximation to oblate spheroids. Note that the asymptotic value for small $\alpha$ is R = 4/15 in both cases, in agreeement with Mavko and Jizba (1991).

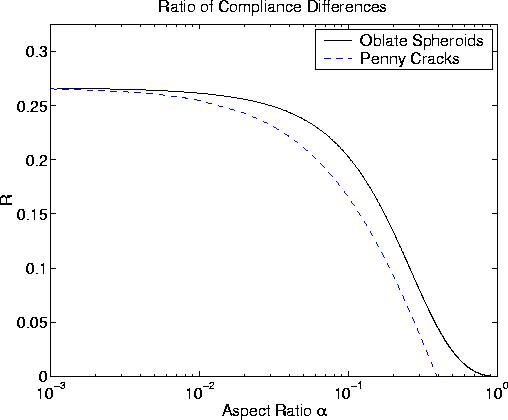
The appropriate expressions for P and Q for oblate spheroids can be found in Berryman (1980b). We repeat the analysis given above in (R2)-(Kdiff) step by step for oblate spheroids. The results are shown in Figure 7, together with the results obtained using the penny-shaped cracks as presented already in Equation (R3). We see that the results agree completely for $\alpha$'s smaller than about 0.001, and are in qualitative agreement over most of the rest of the range. As already discussed, the penny-shaped crack model is a limiting approximation for the oblate spheroids, and deviations from the curve for oblate spheroids do not have physical significance; they merely indicate the degree of error inherent in this choice of approximation scheme. The results for oblate spheroids should be considered rigorous.