




Next: About this document ...
Up: Sava and Biondi: Amplitude-preserved
Previous: Conclusions
- Biondi, B., and Palacharla, G., 1996,
 prestack migration of common-azimuth data: Geophysics, 61, no. 6, 1822-1832.
prestack migration of common-azimuth data: Geophysics, 61, no. 6, 1822-1832.
-
- Biondi, B. L., 1999, 3-D Seismic Imaging: http://sepwww.stanford.edu/sep/bion do/Lectures/index.html.
-
- Biondi, B., 2001, Narrow-azimuth migration: Analysis and tests in vertically layered media: SEP-108, 105-118.
-
- Bleistein, N., and Handelsman, R. A., 1975, Asymptotic expansions of integrals: Rinehart Winston.
-
- Claerbout, J. F., 1995, Basic Earth Imaging: Stanford Exploration Project.
-
- Clayton, R. W., and Stolt, R. H., 1981, A Born-WKBJ inversion method for acoustic reflection data: Geophysics, 46, no. 11, 1559-1567.
-
- de Bruin, C. G. M., Wapenaar, C. P. A., and Berkhout, A. J., 1990, Angle-dependent reflectivity by means of prestack migration: Geophysics, 55, no. 9, 1223-1234.
-
- Fomel, S., 1996, Migration and velocity analysis by velocity continuation: SEP-92, 159-188.
-
- Huang, L., Fehler, M. C., and Wu, R. S., 1999, Extended local Born Fourier migration method: Geophysics, 64, no. 5, 1524-1534.
-
- Ottolini, R., 1982, Migration of reflection seismic data in angle-midpoint coordinates: Ph.D. thesis, Stanford University.
-
- Prucha, M., Biondi, B., and Symes, W., 1999, Angle-domain common-image gathers by wave-equation migration: 69th Ann. Internat. Meeting, Soc. Expl. Geophys., Expanded Abstracts, 824-827.
-
- Prucha, M. L., Clapp, R. G., and Biondi, B. L., 2001, Imaging under salt edges: A regularized least-squares inversion scheme: SEP-108, 91-104.
-
- Rickett, J., 2001, Model-space vs data-space normalization for finite-frequency depth migration: SEP-108, 81-90.
-
- Sava, P., and Biondi, B., 2000, Wave-equation migration velocity analysis: Episode II: SEP-103, 19-47.
-
- Sava, P., and Fomel, S., 2000, Angle-gathers by Fourier Transform: SEP-103, 119-130.
-
- Stolt, R. H., and Benson, A., 1986, Seismic migration -- theory and practice: Geophysical Press, London - Amsterdam.
-
- Stolt, R. H., 1978, Migration by Fourier transform: Geophysics, 43, no. 1, 23-48.
-
- Wapenaar, K., Van Wijngaarden, A., van Geloven, W., and van der Leij, T., 1999, Apparent AVA effects of fine layering: Geophysics, 64, no. 6, 1939-1948.
-
A
This appendix presents a derivation of the expression for the
weighting Jacobian in the case of variable velocity.
The dispersion relation
| 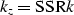 |
(43) |
can be approximated using a Taylor series expansion around
the constant reference slowness (s0):
| 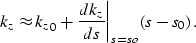 |
(44) |
We then take the derivative of
kz with respect to the frequency 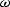
![\begin{displaymath}
\frac{dk_z}{d\omega} =
\frac{d{k_z}_0}{d\omega} +
\frac{d}...
...mega} \left [\frac{d{k_z}_0}{d s} \right ]\left (s-s_0\right ),\end{displaymath}](img87.gif)
and if we note that
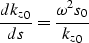
we obtain
| ![\begin{displaymath}
\frac{dk_z}{d\omega} =
\frac{d{k_z}_0}{d\omega} +
\frac{d}...
...left [\frac{\omega^2s_0}{{k_z}_0} \right ]\left (s-s_0\right ).\end{displaymath}](img89.gif) |
(45) |
We continue by evaluating the derivatives with respect to
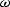 on the right hand side. With little algebra, we obtain
on the right hand side. With little algebra, we obtain
![\begin{displaymath}
\frac{d}{d\omega} \left [\frac{\omega^2s_0}{{k_z}_0} \right ...
...\left (2- \left [\frac{\omega s_0}{{k_z}_0}\right ]^2 \right ).\end{displaymath}](img90.gif)
therefore
| ![\begin{displaymath}
\frac{dk_z}{d\omega} =
\frac{\omega s_0}{{k_z}_0} s_0+
\...
...ac{\omega s_0}{{k_z}_0}\right ]^2 \right )\left (s-s_0\right ).\end{displaymath}](img91.gif) |
(46) |
The prestack weighting Jacobian is:
| ![\begin{displaymath}
\bold W_k_h=
\left [
\frac{\omega s_0}{{k_{\rm zs_0}}} s_0+...
...{k_z}_0}\right ]^2 \right )\left (s_r-s_0\right )
\right ]^{-1}\end{displaymath}](img74.gif) |
(47) |
which, in constant slowness, takes the simple form
| ![\begin{displaymath}
\bold W_k_h=
\left [
\frac{\omega s_0}{{k_{\rm zs_0}}} s_0
+
\frac{\omega s_0}{{k_{\rm zr_0}}} s_0
\right ]^{-1}.\end{displaymath}](img92.gif) |
(48) |





Next: About this document ...
Up: Sava and Biondi: Amplitude-preserved
Previous: Conclusions
Stanford Exploration Project
4/30/2001
![]()
![]()
![]()
![]() on the right hand side. With little algebra, we obtain
on the right hand side. With little algebra, we obtain
![\begin{displaymath}
\frac{d}{d\omega} \left [\frac{\omega^2s_0}{{k_z}_0} \right ...
...\left (2- \left [\frac{\omega s_0}{{k_z}_0}\right ]^2 \right ).\end{displaymath}](img90.gif)
![\begin{displaymath}
\frac{dk_z}{d\omega} =
\frac{\omega s_0}{{k_z}_0} s_0+
\...
...ac{\omega s_0}{{k_z}_0}\right ]^2 \right )\left (s-s_0\right ).\end{displaymath}](img91.gif)
![\begin{displaymath}
\bold W_k_h=
\left [
\frac{\omega s_0}{{k_{\rm zs_0}}} s_0+...
...{k_z}_0}\right ]^2 \right )\left (s_r-s_0\right )
\right ]^{-1}\end{displaymath}](img74.gif)