Warped pinch-out model - test case

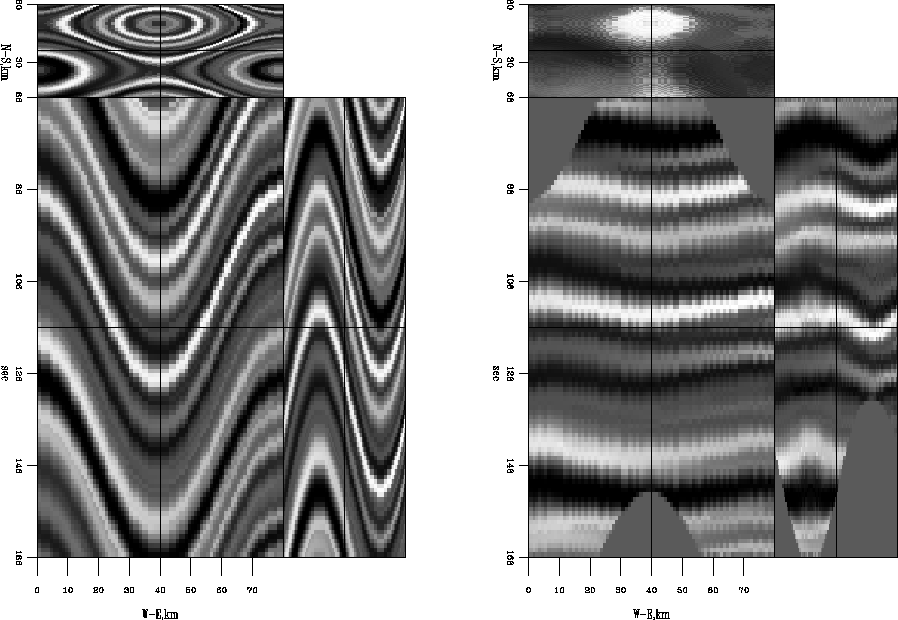
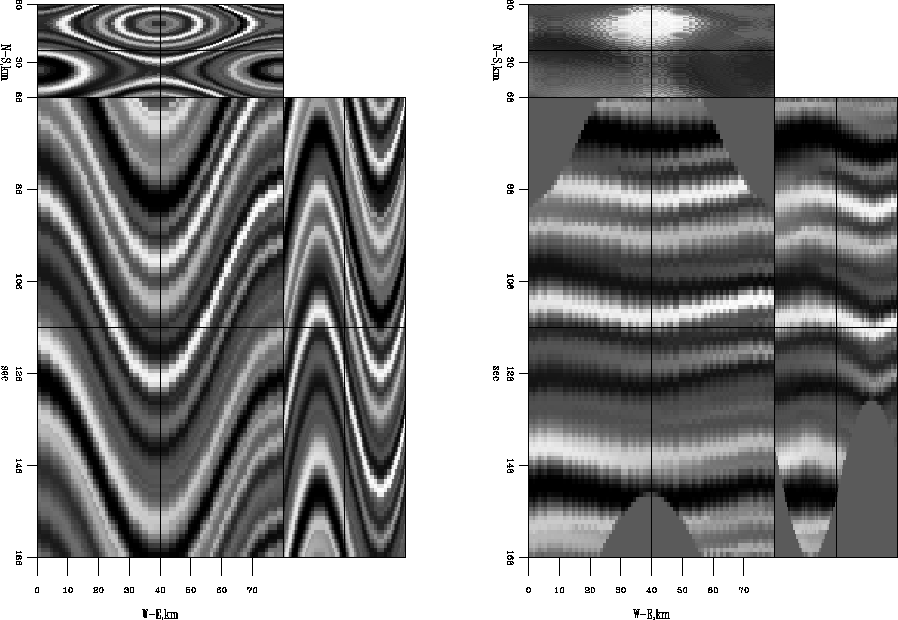
This pinch-out model was created from a series of flat reflectors convolved with wavelets that gradually increase in dominant frequency from one corner of the model to the other. These flat reflectors were then warped with a cosine function. The 2-D and 3-D flattening results are shown in Figures and , respectively. Here, again, both 2-D [equation (5)], and 3-D [equation (7)], integration methods do a similar job. There still is some residual warping in both. Since these flattening methods are operating on time-slices, the subtle pinch-out shifts are too small to be removed with one pass of this method. Also, the smoothing of the dips reduces sensitivity to the pinch-out.

In summary, the pinch-outs in this model are not severe enough to determine how these flattening methods deal with the issues non-unique and replicating solutions. These issues need further evaluation with models that have more dramatic pinch-outs.

 

pinchout_cos.flat_comp2D
Figure 4 Pinch-out model warped by a cosine function. Left is unflattened. Right is flattened using the 2-D integration method described in equation (5).

 

pinchout_cos.flat_comp3D
Figure 5 Same as Figure except using 3-D integration described in equation (7).