NON-HYPERBOLIC MOVEOUT EQUATIONS

In the case of the Byun's approximation the travel time equation was represented into the form

$$t_x^2=t_0^2+({z^2\over v_\gamma}+{x^2\over v_x}){x^2\over {x^2+z^2}}$$ (6)

where $v_\gamma$ represent $(v_x^{-2}+q^{-2})^{-{1\over 2}}$.But in this case, $v_\gamma$ can be replaced by the more physically meaningful parameter, v_q, which is the velocity at 45 degrees. By using v_q, we can formulate the moveout equation as follows:

$$t_x^2=t_0^2({{z^2-x^2}\over {x^2+z^2}})+{x^2\over v_x^2}({{x^2-z^2}\over {x^2+z^2}})+{4\over v_q^2}({{x^2z^2}\over{x^2+z^2}})$$ (7)

where

$$v_q=({1\over 2}{v_z^{-2}}+{1\over 2}{v_x^{-2}}+{1\over 4}{q^{-2}})^{-{1\over 2}}$$

In the case of the Muir's approximation, the moveout equation has the form of

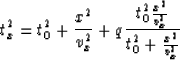$$t_x^2=t_0^2+{x^2\over v_x^2}+q{{t_0^2{x^2\over v_x^2}}\over {t_0^2+{x^2\over v_x^2}}}$$ (8)

In both approximations, q represents the anelliptic factor and set equal to zero gives hyperbolic moveout equation. In the case of Byun's approximation, the anelliptic factor, q or v_q, directly represents the deviated velocity from the ellipse or the velocity at 45 degrees, respectively. In the case of Muir's approach, the unit of q has no dimension, and the magnitude is controlled by the ratio of horizontal velocity to vertical velocity.

From a practical point of view, Muir's method is superior because it can be used for surface common midpoint gather data by fixing time for some event and applying semblance analysis as a function of q and v_x. Byun's approach requires one more parameter, v_z, to calculate moveout. For a given event, therefore, semblance analysis can be performed by scanning over ranges of the three parameters, v_z,v_x and v_q. If the average vertical velocity v_z is known, as may the case from VSP or check-shot data, then the semblance scan can be done over the two parameters, v_x and v_q.