Electromagnetic field equations

In deriving the electromagnetic coupled field equations we make the assumption that within the medium the divergence of the electric stress field is zero (${\rm \bf div}~{\bf \sigma_2} = 0$), i.e. that there are no ``batteries'' buried in the medium. Making this assumption is equivalent to setting the forcing term in Equation 5 to zero. We note that the magnetic fields and magnetic induction are related by the magnetic permeability $\mu$ (${\bf B} = \displaystyle \mathop{\mbox{${\bf \mu}$}}_{\mbox{$\sim$}} {\bf H}$). Since there is no magnetic monopole, divergence of the magnetic field is also zero (div B=0). If we allow electric current to flow, the current density ${\bf j}$ is related to the electric stress field by the conductivity $$\mathop{\mbox{${\bf \kappa_e}$}}_{\mbox{$\sim$}}$$ as follows:

$${\bf j}~=~ \displaystyle \mathop{\mbox{${\bf \kappa_e}$}}_{\mbox{$\sim$}} ~{\bf \sigma_2}$$ (9)

We can use Maxwell's equation to describe the relation ship between electric and magnetic fields:

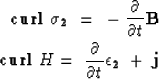$$\begin{eqnarray} {\rm \bf curl}~{\bf \sigma_2}~=~- {\partial \over{\partial t}} ... ... curl}~H =~{\partial \over{\partial t}} {\bf \epsilon_2}~+~{\bf j}\end{eqnarray}$$ (10) (11)

The linear law relating electric stress components to components of elastic strain, electric and thermal displacements is now

$${\bf \sigma_2}~=~ \displaystyle \mathop{\mbox{${\bf c_{21}}$... ..._{\mbox{$\sim$}} ~~{\partial \over{\partial t}}{\bf \epsilon_3}$$ (12)

Consequently, in terms of electric displacements, we end up with the coupled electromagnetic field equations  

$$- {\rm \bf curl}~ \displaystyle \mathop{\mbox{${\bf \mu^{-1}... ...}}_{\mbox{$\sim$}} ~{\partial \over{\partial t}} {\bf \sigma_2}$$ (13)