




Next: An equivalent medium toolkit
Up: IMPLEMENTATION
Previous: IMPLEMENTATION
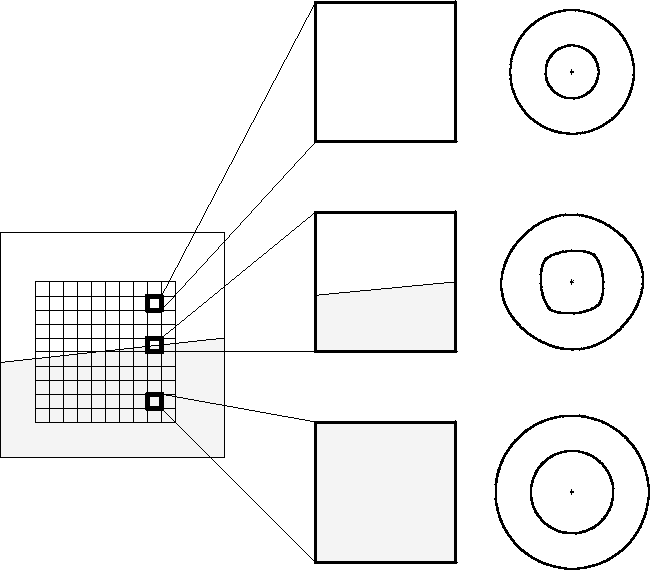
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a medium consisting of two homogeneous regions
separated by a gently dipping boundary. A 10 by 10 grid of cells has
been laid down on the medium. We want to find the appropriate elastic
constants to assign to each cell. There are three sorts of cells to
consider; we have highlighted one of each kind.
shows a medium consisting of two homogeneous regions
separated by a gently dipping boundary. A 10 by 10 grid of cells has
been laid down on the medium. We want to find the appropriate elastic
constants to assign to each cell. There are three sorts of cells to
consider; we have highlighted one of each kind.
The top highlighted cell is entirely within the top medium. Its elastic
constants are therefore the same as that of the top (light-colored)
homogeneous medium. To the right of the blown-up cell we show the P-SV
impulse response for this medium. The bottom highlighted cell is
entirely in the lower medium, and so its elastic constants are the same
as that of the lower (dark-shaded) homogeneous medium. Again, to the
right we show the P-SV impulse reponse.
tilt
Figure 1
Left: A sampling grid laid down on a medium made up of two homogeneous blocks.
Three representative grid cells have been highlighted.
Center column: Expanded views of the three representative grid cells.
Right column: P-SV impulse responses of the homogeneous
equivalent medium for each expanded grid cell.

The middle highlighted cell is the interesting one, since it contains a
mixture of both media. Intuitively, the elastic constants for this
cell should be some sort of average of the top and bottom media. We
perform the average by considering the cell to be a bit of a tilted
layered media, with the proportions of each of the two media set in
accordance with the area of each in the grid cell. We then use S&M
theory to find the homogeneous equivalent to this particular tilted
layered media. To the right we show the resulting
transversely-isotropic P-SV impulse response of this cell. Note the
axis of symmetry is normal to the tilted layer boundary within the
cell.
The only step left to specify in our interpolation algorithm is how to
determine the effective elastic constants of a layered-medium grid cell
using S&M theory.





Next: An equivalent medium toolkit
Up: IMPLEMENTATION
Previous: IMPLEMENTATION
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a medium consisting of two homogeneous regions
separated by a gently dipping boundary. A 10 by 10 grid of cells has
been laid down on the medium. We want to find the appropriate elastic
constants to assign to each cell. There are three sorts of cells to
consider; we have highlighted one of each kind.
shows a medium consisting of two homogeneous regions
separated by a gently dipping boundary. A 10 by 10 grid of cells has
been laid down on the medium. We want to find the appropriate elastic
constants to assign to each cell. There are three sorts of cells to
consider; we have highlighted one of each kind.