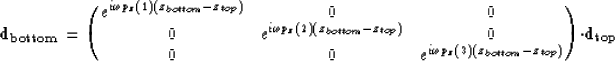Next: Calculation of reflection and
Up: TWO WAY PHASE SHIFT
Previous: TWO WAY PHASE SHIFT
I compute the propagation of waves in 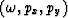 space in a
homogeneous medium by phase shifting in depth. Given a wavefield at
some depth z0,
space in a
homogeneous medium by phase shifting in depth. Given a wavefield at
some depth z0, 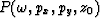 the wavefield at another
depth, z, can be expressed as a phase shifted version of this
wavefield.
the wavefield at another
depth, z, can be expressed as a phase shifted version of this
wavefield.
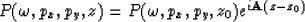
In general the operator 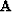 is a matrix operator
but if the wavefield, P is expressed as a vector of amplitudes of
the different wavetypes the operator A is diagonal. The different
wavetypes are the eigensolutions of the Christoffel equation (see
appendix) so the operator is diagonalized. For each of the six
wavetypes the extrapolation in depth can be expressed as,
is a matrix operator
but if the wavefield, P is expressed as a vector of amplitudes of
the different wavetypes the operator A is diagonal. The different
wavetypes are the eigensolutions of the Christoffel equation (see
appendix) so the operator is diagonalized. For each of the six
wavetypes the extrapolation in depth can be expressed as,
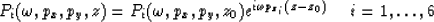
Thus, once I have calculated the wave amplitudes at the top of any layer I can
calculated the amplitudes at the bottom of the layer by phase shifting the
data. The value of pz is the same for all frequencies but the phase
shift through the layer for each frequency is given by.
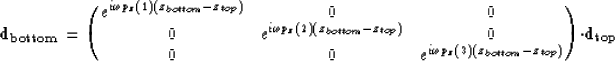
This calculation is different for each frequency but on a vector computer it
is fully vectorized over frequency.
If I am ``turning off'' propagation of a particular wavetype it is at this
stage that I do it. I can simply zero the amplitude of the wave instead of
applying the shifting operator.





Next: Calculation of reflection and
Up: TWO WAY PHASE SHIFT
Previous: TWO WAY PHASE SHIFT
Stanford Exploration Project
12/18/1997
![]()
![]()