




Next: Proposed Canonical Forms for
Up: CANONICAL FORMS
Previous: Form Invariance under Rotation
What angle to choose? From the point of view of parsimony we can reduce the
number of variables from 13 to 12 by rotating our coordinate system around
the 3-axis by an angle = 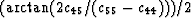 . This will
anihilate the two occurences of the c45 term.
. This will
anihilate the two occurences of the c45 term.
|  |
(4) |
Does this make sense physically? Yes. Since there is 2-fold symmetry, the three
waves propagating along the 3-axis have orthogonal directions of particle
motion, and those directions corresponding to the two pure shear waves define
two pseudo-symmetry axes. If the coordinate system is now aligned along these
axes, the c45 term disappears,





Next: Proposed Canonical Forms for
Up: CANONICAL FORMS
Previous: Form Invariance under Rotation
Stanford Exploration Project
12/18/1997

