ORTHOGONAL RELATION

The eikonal equation in two dimensions relates the two gradient components of the traveltime field:  

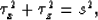$$\tau^2_x+\tau^2_z = s^2,$$ (1)

where s is a two-dimensional slowness model and $\tau$ is the traveltime field. Subscripts x and z denote partial derivatives with respect to x and z, respectively. Using a finite-difference method, one can solve this equation for $\tau$. The contour lines of $\tau$ define the trajectories of wavefronts. It is well known that, in an isotropic medium, the trajectories of rays are always perpendicular to the trajectories of wavefronts and that the gradient directions of a field are always perpendicular to the contour lines of the field. Therefore, the gradient of $\tau$ is orthogonal to the gradient of function p whose contour lines are the trajectories of rays:

$$\hbox{grad} [\tau] \cdot \hbox{grad} [p] = 0.$$

If we assume that the traveltime field $\tau$ is known, this equation leads to an linear, first-order partial differential equation for p  

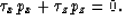$$\tau_x p_x + \tau_z p_z = 0.$$ (2)

In the following sections, I will explain how to solve this equation for two specific cases.