Example

I choose Van Trier's method to solve the eikonal equation in the polar coordinates because this method gives the traveltime derivatives that appear in the orthogonal equation. If Vidale's method is used, these derivatives have to be numerically computed from the traveltime field. Once the traveltime derivatives are known, equation (4) becomes a first-order, linear partial-differential equation and is readily solved using the standard finite-difference techniques. After p has been computed, the coordinates of the ray that connects the source location to any given point can be found by tracing the contour line starting from the given point. It is guaranteed that all contour lines of field p will end at the source location.

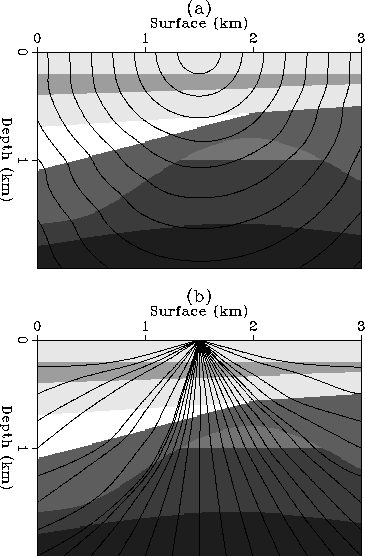
I test the method on a synthetic slowness model. The results are shown in Figure . The raster images of the synthetic slowness model are overlain with the wavefronts and rays. The wavefronts are plotted at a constant time-interval. The rays are traced to the destinations distributed uniformly along the boundaries of the model. The ray-bending effects are clearly seen.

 

point
Figure 1 Ray tracing for a point source: (a) wavefronts; (b) rays. The background shows the slowness model. High intensities denote high velocities or low slowness.