Next: Conclusions
Up: Zhang: DMO
Previous: DEFINITIONS OF DMO
Using traveltime relations, I generated synthetic constant offset
sections that contain events reflected from plane reflectors. The velocity
is 2000 m/s. I chose five offsets ranging from 0 to 2000 m. The
dips of the reflectors vary from 0 to 80 degrees in increments of 20
degrees. I assume that these sections can be
processed with spherical divergence and attenuation corrections
so that the peak amplitudes of the wavelets are proportional
to the reflection coefficients at the depth points
from which these wavelets were reflected.
It is important to preserve this proportionality after NMO and DMO corrections.
In my examples, I further assume that the reflection coefficients
are constant along the reflectors and are independent of the angles of rays.
(Although this assumption is unrealistic, it simplifies the explanation
of the results.) In accordance with these assumptions, the ideal outputs of the DMO
operator should have a constant peak value for all the wavelets.
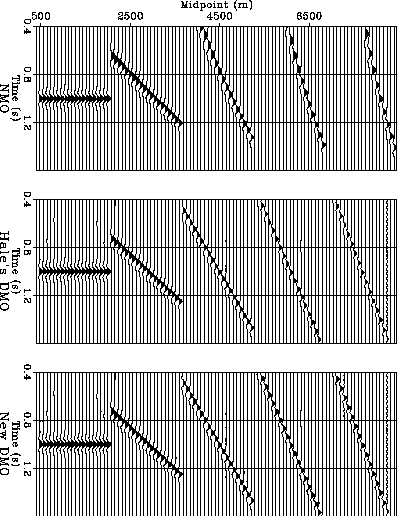
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) displays constant offset sections with a fixed offset
of 2000 meters. The top panel shows the result after the NMO corrections:
the peak amplitudes of the wavelets should be constant.
This is because NMO is a time-stretching operation that changes the shapes of
wavelets but not their peak values.
The middle panel shows the output of Hale's DMO operator: the amplitudes
of the wavelets decrease as the dips of the reflector increase.
Because the sections are small windows near the centers of large sections,
the possibility of boundary effects can be ruled out.
Therefore, we can conclude that this operator attenuates events with large dips.
The bottom panel shows the result after applying uniform-amplitude
DMO operator: the peak amplitudes of the wavelets are constant.
displays constant offset sections with a fixed offset
of 2000 meters. The top panel shows the result after the NMO corrections:
the peak amplitudes of the wavelets should be constant.
This is because NMO is a time-stretching operation that changes the shapes of
wavelets but not their peak values.
The middle panel shows the output of Hale's DMO operator: the amplitudes
of the wavelets decrease as the dips of the reflector increase.
Because the sections are small windows near the centers of large sections,
the possibility of boundary effects can be ruled out.
Therefore, we can conclude that this operator attenuates events with large dips.
The bottom panel shows the result after applying uniform-amplitude
DMO operator: the peak amplitudes of the wavelets are constant.
nmodmodip
Figure 2 Common offset sections. Top: after NMO correction; middle: after the
conventional DMO correction; bottom: after the uniform-amplitude DMO
correction. The offset is 2000 meters, and the dips of the reflectors
are 0, 20, 40, 60, 80 degrees.

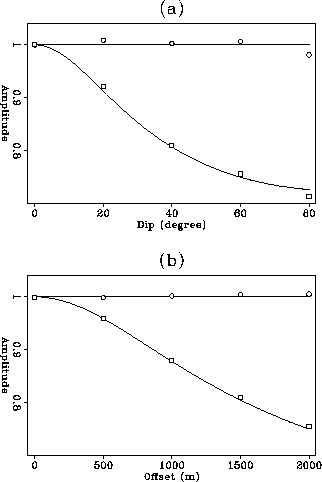
A better way to visualize the contrast between the outputs of the two DMO
operators is to plot the peak amplitude of the wavelets
as a function of offset and dip, as shown in
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and
a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
Evidently, uniform-amplitude DMO works as suggested. The
amplitude curves are almost constant for all dips and offsets.
With Hale's DMO, however, the amplitude curves drop down to about 50%
when the dip is 80 degrees or the offset is 2000 meters.
b.
Evidently, uniform-amplitude DMO works as suggested. The
amplitude curves are almost constant for all dips and offsets.
With Hale's DMO, however, the amplitude curves drop down to about 50%
when the dip is 80 degrees or the offset is 2000 meters.
ampvall
Figure 3 The peak amplitude of the wavelets as the function of (a) the dip of
a reflector with an offset of 2000 meters, (b) the offset of the experiment with
a dip angle of 60 degrees. The samples are picked from the wavelets
at the centers of the sections.
The circles indicate samples
associated with uniform-amplitude DMO;
the squares indicate samples
associated with conventional DMO. The continuous curves are calculated
with the analytical formulae of Black and Schleichor (1990).






Next: Conclusions
Up: Zhang: DMO
Previous: DEFINITIONS OF DMO
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) displays constant offset sections with a fixed offset
of 2000 meters. The top panel shows the result after the NMO corrections:
the peak amplitudes of the wavelets should be constant.
This is because NMO is a time-stretching operation that changes the shapes of
wavelets but not their peak values.
The middle panel shows the output of Hale's DMO operator: the amplitudes
of the wavelets decrease as the dips of the reflector increase.
Because the sections are small windows near the centers of large sections,
the possibility of boundary effects can be ruled out.
Therefore, we can conclude that this operator attenuates events with large dips.
The bottom panel shows the result after applying uniform-amplitude
DMO operator: the peak amplitudes of the wavelets are constant.
displays constant offset sections with a fixed offset
of 2000 meters. The top panel shows the result after the NMO corrections:
the peak amplitudes of the wavelets should be constant.
This is because NMO is a time-stretching operation that changes the shapes of
wavelets but not their peak values.
The middle panel shows the output of Hale's DMO operator: the amplitudes
of the wavelets decrease as the dips of the reflector increase.
Because the sections are small windows near the centers of large sections,
the possibility of boundary effects can be ruled out.
Therefore, we can conclude that this operator attenuates events with large dips.
The bottom panel shows the result after applying uniform-amplitude
DMO operator: the peak amplitudes of the wavelets are constant.