NUMERICAL EXAMPLES

To compare the proposed interpolation scheme with Spitz`s method, I applied the scheme to a data set which was similar to that used by Spitz (1991, Spitz). Figure 2 shows synthetic data which is spatially aliased linear events with random noises, and the result of first-order interpolation. The result is comparable to that of Spitz. Figure 3 shows the spectra of data before and after interpolation. The spectrum after interpolation fits well to our guess which can be intuitively conjectured from the original spectrum.

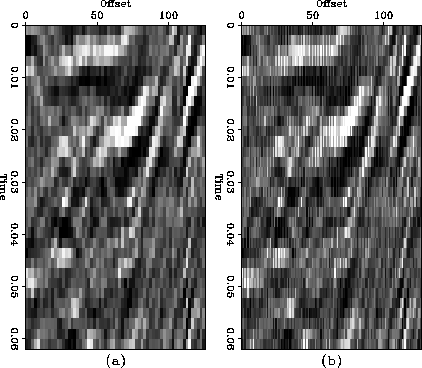
For a more realistic test, I have applied the interpolation scheme to a real dataset which has aliased events. The dataset, a 24-fold CMP stack of NMO-corrected Western offshore Texas data, has been windowed to provide a smaller test dataset. Figure 4 illustrates the performance of the interpolation scheme proposed. It shows that the proposed algorithm may accommodate curvatures and lateral amplitude variation.

 

fig2
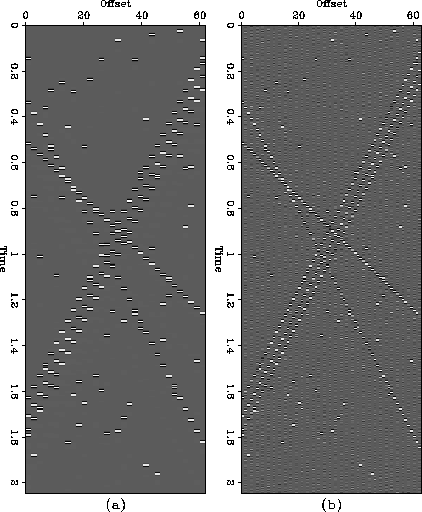
Figure 2 (a)Input data made of three aliased linear events (b) First order interpolated data. Note that the parallel events have been correctly interpolated.

 

fig3
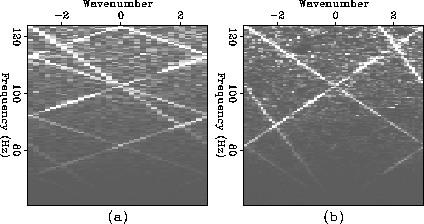
Figure 3 Amplitude f-k spectra. The horizontal axes represent normalized wavenumber, from -0.5 to 0.5 cycles. (a)f-k amplitude spectrum of the input shown in Figure 2(a). The unit scale of the normalized wavenumber is 1/32 cycles. (b) f-k amplitude spectrum of the interpolated data set shown in Figure 2(b). The unit scale of the normalized wavenumber is 1/64 cycles.

 

fig4
Figure 4 (a)Input data which has windowed from a CMP stack. (b) First order interpolated data.