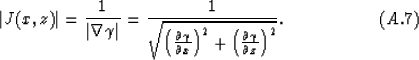Next: APPENDIX B
Up: Zhang: F-D calculation
Previous: References
In this appendix, I derive the formula for calculating the Jacobian function
J(x,z) and the partial differential equation (14).
From equation (12), we have
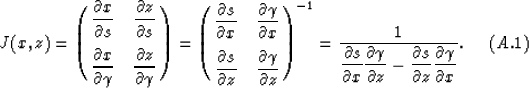
The expression in the denominator of the last line is a cross-product
of two gradient vectors:
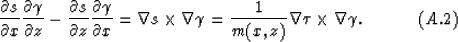
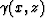 is the take-off angle of the ray that
reaches point(x,z), and is constant along each ray. Thus,
the gradient directions of
is the take-off angle of the ray that
reaches point(x,z), and is constant along each ray. Thus,
the gradient directions of 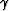 are always orthogonal to rays. On
the other hand, the gradient directions of traveltimes are always
tangential to rays. Consequently,
are always orthogonal to rays. On
the other hand, the gradient directions of traveltimes are always
tangential to rays. Consequently, 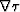 and
and 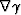 are
orthogonal, which yields
are
orthogonal, which yields

and

In 2-D, equation (A.3) can be rewritten as

which is equation (14). From equations (A.1), (A.2) and (A.4),
we can derive

The eikonal equation states that 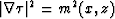 or
or
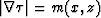 . Applying this relation to equation (A.6), we get
equation (12):
. Applying this relation to equation (A.6), we get
equation (12):
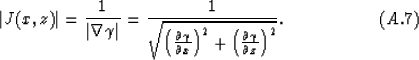





Next: APPENDIX B
Up: Zhang: F-D calculation
Previous: References
Stanford Exploration Project
12/18/1997
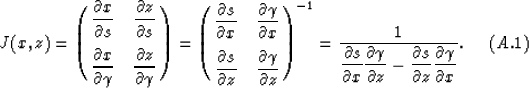
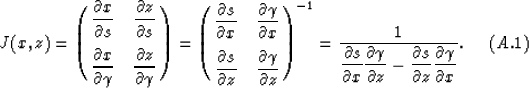
![]()
![]()
![]()
![]()
![]()