




Next: Representation of the slowness
Up: DISCUSSION
Previous: DISCUSSION
If we assume that the slowness model has a constant value m0 in the region
around source position (xs,zs), we can use the following initial
conditions for the local paraxial ray method. The traveltimes are
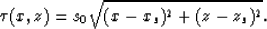
The ray directions are specified by the angles of rays
to the vertical, as follows:
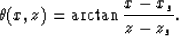
We can also find that
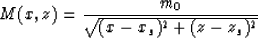
and
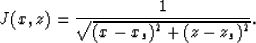
If the slowness varies in this region, the paraxial ray method should be used
to find the initial conditions.





Next: Representation of the slowness
Up: DISCUSSION
Previous: DISCUSSION
Stanford Exploration Project
12/18/1997
![]()
![]()
![]()
![]()