In terms of known and missing data

Alternatively, changing geometrical bases can be viewed as estimating missing data from known data. Subscripts _m denote missing and _k denote known data or model values. Identifying $\bf S_1$ with the known portion and $\bf S_2$ with the unknown portion of the data, we see directly that equation (3) is an estimation of unknown data (at the new geometry).

 

$${\bf d_k}(x,t) = {\bf S_k}~{\bf (S^t_k~ S_k )^{-1} }~ {\bf S_k^t}~ {\bf d_k(x,t)}$$ (4)

 

$${\bf d_m}(x,t) = {\bf S_m}~{\bf (S^t_k~ S_k )^{-1} }~ {\bf S_k^t}~ {\bf d_k(x,t)} .$$ (5)

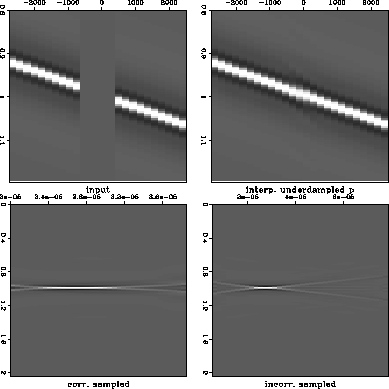
Given a line in x-t with a gap in the middle, it is easy to demonstrate the null space problem. We run into that problem when the domain is not finely enough sampled in p, or in other words the model space is underdetermined.

Figure shows a line with a bandlimited spike. The least squares forward transform incorporates the information about the gap into the operator. The slant stack domain shows clearly a single spike for the properly sampled data.

 

inadequate
Figure 1 Inadequate sampling in ray parameter leaves problem underdetermined. The least squares approach still recovers original data very well but looks for a minimum length solution in the underdetermined area. It might be hard to see but known amplitudes are reconstructed perfectly, while amplitudes that lie in the gap are smoothly decreasing towards the middle of the gap. A perfect reconstruction would place constant known amplitudes into the gap.