 |
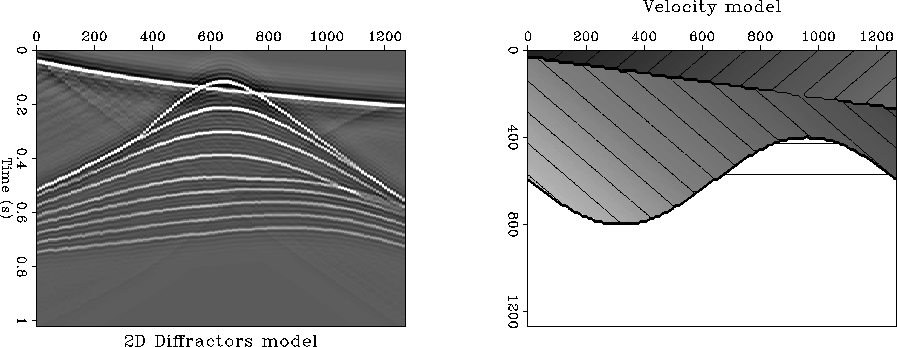
Figure 2 The two dimensional diffraction model and the velocity model.
In Figure 2 the diffraction model is shown on a 128x256 grid, together with the velocity model. The model is obtained by simulating the dipping event as an assembly of point scatterers. The travel-times to each point scatterer are calculated using an adaptive step finite-differences travel-time algorithm (Van Trier and Symes, 1991).
 |
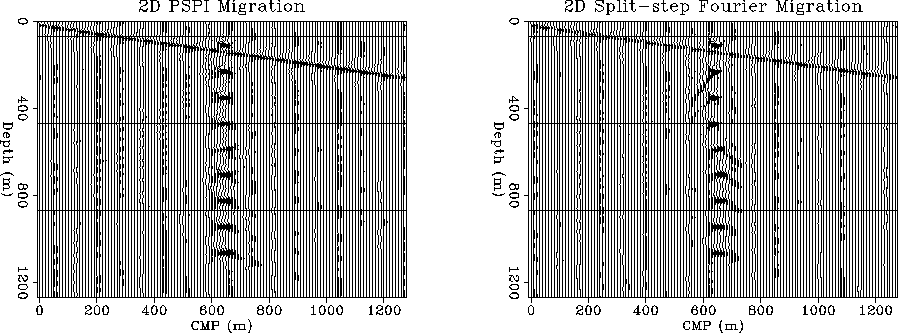
Running several velocity models and comparing the migration results between the two methods, the PSPI appears to perform better than then Split-step in the presence of lateral velocity discontinuities. This difference is to be expected as the error in the Split-step algorithm is proportional with the second order slowness perturbation. In media with smooth lateral velocity changes the two methods offer very similar results.
In Figure 3, the second diffractor from the top is less focused in the migration result of the Split-step algorithm, due to the velocity discontinuity along the dipping event. PSPI handles better velocity discontinuities and even though it has the option of splitting the velocity interval in more than two velocities and it appears that very little is gained by using more velocities for the downward extrapolation step.
 |