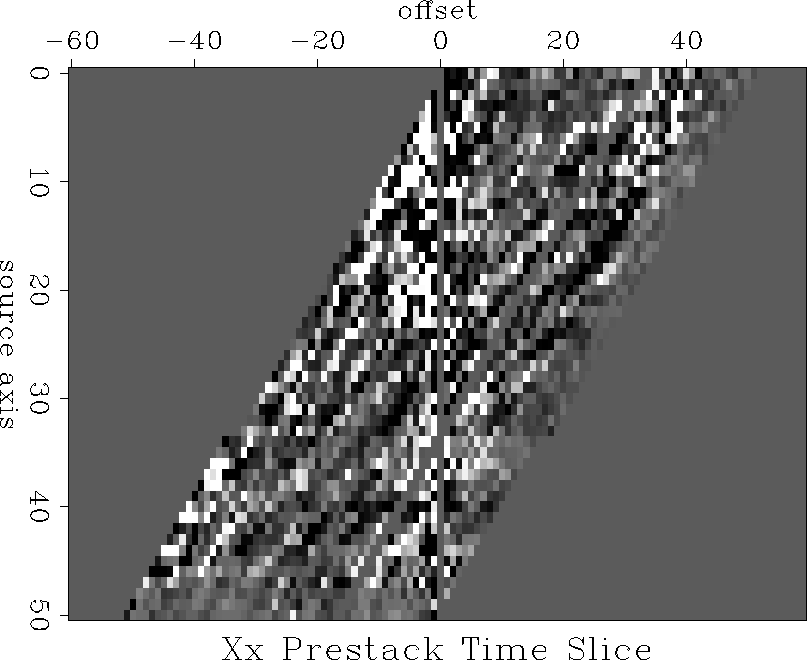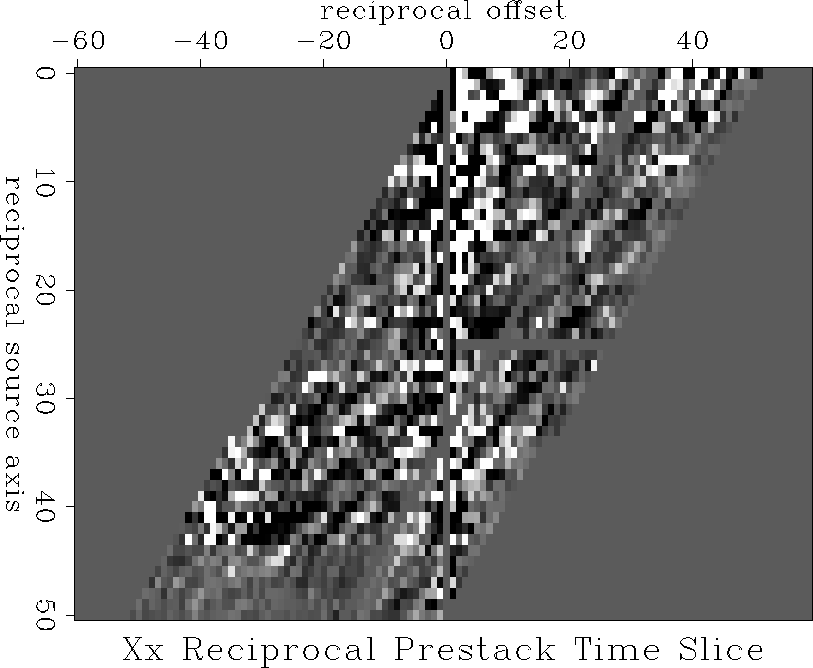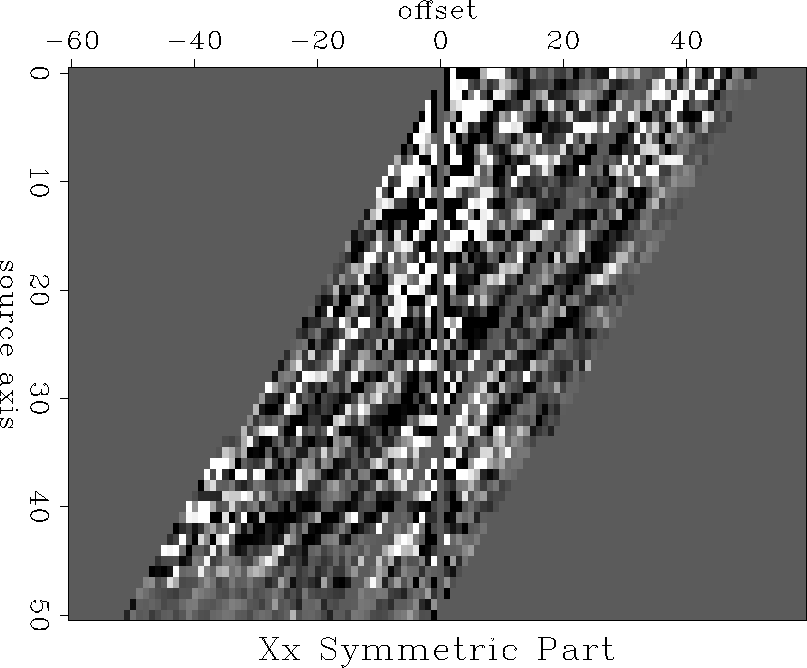Next: THE OPTIMIZATION PROBLEM
Up: SYMMETRIZING THE WAVE FIELD
Previous: Wave field types
The premise of reciprocal acquisition geometry is intimately related to
symmetric data acquisition.
The idea of symmetric wave field sampling was described by Ongkiehong
1988 and Vermeer .
Their recommendation is to record seismic data as generally
as possible and perform
data reduction later, in the processing step. Array forming is thus done
not in the field but on the computer. This method, of course,
requires sufficient
dynamic range of recording equipment, but does not discriminate
against propagation effects.
Data are most unbiased if they are collected symmetrically, that is, for each
(vector) source throughout the survey we must have a (vector) receiver
at the same location.
Ongkiehong and Vermeer show asymmetric sampling examples and their effects
on stack arrays.
The effect can be seen on the changes in amplitude changes with offset
during migration and inversion.
The acquisition geometry issue is independent of
the type of experiment carried out and applies to scalar,
as well as vector field, experiments. Symmetric sampling is a general notion
and offers general guidelines for processing.
Their conclusion is that symmetric acquisition geometry
offers the best unbiased acquisition and allows the most flexibility
in later preprocessing. I'd like to extend their observation and claim
that reciprocal acquisition geometry offers the best unbiased acquisition
and allows new directions in processing that data.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are examples of nearly reciprocal
data acquisition. Figure
are examples of nearly reciprocal
data acquisition. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) plots the source and receiver
positions of a prestack multi-component data set. Besides one source gap, the
acquisition geometry is regular. Each source is located
between a receiver
position. Figure
plots the source and receiver
positions of a prestack multi-component data set. Besides one source gap, the
acquisition geometry is regular. Each source is located
between a receiver
position. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represent the symmetric
and antisymmetric components of a time slice through the prestack data set.
Source and geophone positions were interpolated by nearest neighbours before
determining the amount of symmetry and deviation. The surprising result is
that the symmetric part and the symmetric part are about the same magnitude.
One would not expect this, if one thought that equation (2) holds
for this data set. The lack of symmetry (or reciprocity) demands some
explanation. I chose to explain it by differences in source behavior,
assuming that differences in receiver behavior are small compared to the
potentially nonlinear behavior of seismic sources. The lack of symmetry
can be employed to set up a minimization problem, where the objective function
maximizes symmetry in a source-location and source-component consistent way.
represent the symmetric
and antisymmetric components of a time slice through the prestack data set.
Source and geophone positions were interpolated by nearest neighbours before
determining the amount of symmetry and deviation. The surprising result is
that the symmetric part and the symmetric part are about the same magnitude.
One would not expect this, if one thought that equation (2) holds
for this data set. The lack of symmetry (or reciprocity) demands some
explanation. I chose to explain it by differences in source behavior,
assuming that differences in receiver behavior are small compared to the
potentially nonlinear behavior of seismic sources. The lack of symmetry
can be employed to set up a minimization problem, where the objective function
maximizes symmetry in a source-location and source-component consistent way.
sgplot
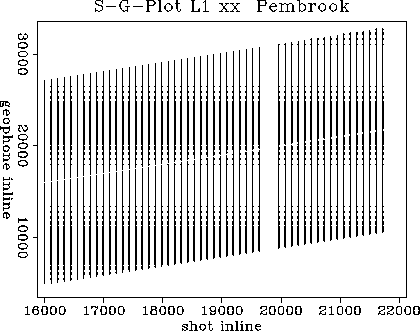
Figure 2 Pembrook 9-c data acquisition geometry is
shown in source and receiver coordinates. This space is identical for all
components. The recording is very regular, and nearly reciprocal.
The source coordinates are between receiver coordinates.




 slicexx1
slicexx1
Figure 3 Time slices of the part of the data for which reciprocal data exist for 50 source points (Xx-component). To go through time slices, press the button.




 slicexx2
slicexx2
Figure 4 Reciprocal time slices of the part of the data for which reciprocal data exist for 50 source points (Xx component). To go through time slices, press the button.




 symslicexx
symslicexx
Figure 5 Symmetric part of the data (Xx-component). To go through time slices press the button.




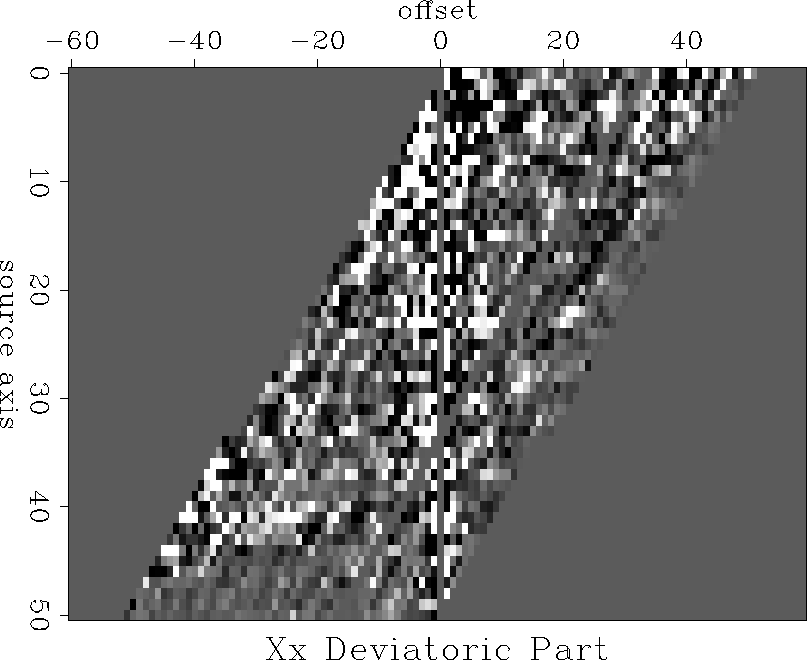
 devslicexx
devslicexx
Figure 6 Antisymmetric part of the data (Xx-component). To go through time slices, press the button.










Next: THE OPTIMIZATION PROBLEM
Up: SYMMETRIZING THE WAVE FIELD
Previous: Wave field types
Stanford Exploration Project
11/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are examples of nearly reciprocal
data acquisition. Figure
are examples of nearly reciprocal
data acquisition. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) plots the source and receiver
positions of a prestack multi-component data set. Besides one source gap, the
acquisition geometry is regular. Each source is located
between a receiver
position. Figure
plots the source and receiver
positions of a prestack multi-component data set. Besides one source gap, the
acquisition geometry is regular. Each source is located
between a receiver
position. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represent the symmetric
and antisymmetric components of a time slice through the prestack data set.
Source and geophone positions were interpolated by nearest neighbours before
determining the amount of symmetry and deviation. The surprising result is
that the symmetric part and the symmetric part are about the same magnitude.
One would not expect this, if one thought that equation (2) holds
for this data set. The lack of symmetry (or reciprocity) demands some
explanation. I chose to explain it by differences in source behavior,
assuming that differences in receiver behavior are small compared to the
potentially nonlinear behavior of seismic sources. The lack of symmetry
can be employed to set up a minimization problem, where the objective function
maximizes symmetry in a source-location and source-component consistent way.
represent the symmetric
and antisymmetric components of a time slice through the prestack data set.
Source and geophone positions were interpolated by nearest neighbours before
determining the amount of symmetry and deviation. The surprising result is
that the symmetric part and the symmetric part are about the same magnitude.
One would not expect this, if one thought that equation (2) holds
for this data set. The lack of symmetry (or reciprocity) demands some
explanation. I chose to explain it by differences in source behavior,
assuming that differences in receiver behavior are small compared to the
potentially nonlinear behavior of seismic sources. The lack of symmetry
can be employed to set up a minimization problem, where the objective function
maximizes symmetry in a source-location and source-component consistent way.