




Next: Example
Up: Ji: Conjugate RTM
Previous: Introduction
In order to find a conjugate operator,
the forward modeling operator must be formulated explicitly.
The acoustic wave equation in the one dimensional space is
| 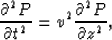 |
(1) |
where P is pressure field, v is the velocity, t and z are
time and depth axis, respectively.
Approximating the derivatives by finite differences, equation (1) becomes
| 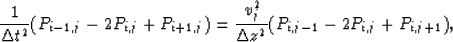 |
(2) |
where i and j represent time and depth indices, respectively.
By rearranging equation (2) for time-extrapolation,
we get the following equation:
| 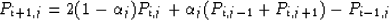 |
(3) |
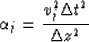
The differencing star in equation (3) covers
the (t,z) space along the z-axis to extrapolate in time
as shown schematically by Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
rt1dmdl
Figure 1 Schematic for time extrapolation modeling
for 1-D acoustic wave equation.
The input is a source function at t=0 and
the output is a trace at z=0.
|
| 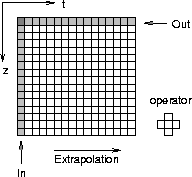 |

To make the operator small enough to show on a page,
I choose a small space like (t,z) = (4,5).
The time extrapolation shown in equation (3) can be
formulated algebraically as follows
| ![\begin{displaymath}
\left[
\begin{array}
{cccc}
\bf S_1&\bf S_2&\bf S_3&\bf S_4\...
...y}\right]
=
\left[
\begin{array}
{c}
{\bf d}\end{array}\right],\end{displaymath}](img5.gif) |
(4) |
where 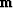 is the model vector at t=1 with length 5,
is the model vector at t=1 with length 5,
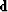 is the data vector with length 4,
and
is the data vector with length 4,
and 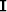 and
and  represent 5 by 5 identity and zero matrices.
The matrix
represent 5 by 5 identity and zero matrices.
The matrix 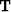 in equation (4) represents tridiagonal matrix
which looks like:
in equation (4) represents tridiagonal matrix
which looks like:
| ![\begin{displaymath}
\left[
\begin{array}
{ccccc}
2(1-\alpha_1)&\alpha_1&0&0&0\\ ...
...)&\alpha_4\\ 0&0&0&\alpha_5&2(1-\alpha_5)\\ \end{array}\right],\end{displaymath}](img11.gif) |
(5) |
where 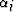 was shown in equation (3).
The matrix
was shown in equation (3).
The matrix 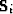 samples the wave field on the surface at i-th time
and has the following form:
samples the wave field on the surface at i-th time
and has the following form:
| ![\begin{displaymath}
{\bf S_1}=
\left[
\begin{array}
{ccccc}
1&0&0&0&0\\ 0&0&0&0&...
...1&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ \end{array}\right],
\dots .\end{displaymath}](img14.gif) |
(6) |
Now, reverse-time migration as the conjugate operator
to the forward time-extrapolation becomes clear.
It is obtained by transposing the operator in equation (4)
and has the following form :
| ![\begin{displaymath}
\left[
\begin{array}
{cccc}
\bf I&\bf 0&\bf 0&\bf 0\\ \end{a...
...
=
\left[
\begin{array}
{c}
{\bf \tilde m}\\ \end{array}\right]\end{displaymath}](img15.gif) |
(7) |
where 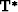 and
and 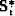 are transpose matrices
of
are transpose matrices
of 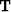 and
and 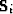 .It is interesting that the conjugate algorithm follows
the reverse-time extrapolation but with an operator which differs
from the forward-time extrapolation.
Instead of using wave fields from the two previous time steps together
for an extrapolation,
the conjugate operator uses the wave fields of
the two previous time steps separately.
The code for this algorithm, which has passed the dot-product test
(Claerbout, 1992), is listed in the Appendix.
.It is interesting that the conjugate algorithm follows
the reverse-time extrapolation but with an operator which differs
from the forward-time extrapolation.
Instead of using wave fields from the two previous time steps together
for an extrapolation,
the conjugate operator uses the wave fields of
the two previous time steps separately.
The code for this algorithm, which has passed the dot-product test
(Claerbout, 1992), is listed in the Appendix.





Next: Example
Up: Ji: Conjugate RTM
Previous: Introduction
Stanford Exploration Project
11/17/1997
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

![\begin{displaymath}
\left[
\begin{array}
{cccc}
\bf S_1&\bf S_2&\bf S_3&\bf S_4\...
...y}\right]
=
\left[
\begin{array}
{c}
{\bf d}\end{array}\right],\end{displaymath}](img5.gif)
![\begin{displaymath}
\left[
\begin{array}
{ccccc}
2(1-\alpha_1)&\alpha_1&0&0&0\\ ...
...)&\alpha_4\\ 0&0&0&\alpha_5&2(1-\alpha_5)\\ \end{array}\right],\end{displaymath}](img11.gif)
![\begin{displaymath}
{\bf S_1}=
\left[
\begin{array}
{ccccc}
1&0&0&0&0\\ 0&0&0&0&...
...1&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ \end{array}\right],
\dots .\end{displaymath}](img14.gif)
![\begin{displaymath}
\left[
\begin{array}
{cccc}
\bf I&\bf 0&\bf 0&\bf 0\\ \end{a...
...
=
\left[
\begin{array}
{c}
{\bf \tilde m}\\ \end{array}\right]\end{displaymath}](img15.gif)