Accuracy

I examine the accuracy of the local ray-tracing method with three synthetic velocity models. The first one is a constant gradient velocity model shown in Figure . The velocity is 1. km/s at the upper-left corner of the model. The magnitude of the velocity gradient is 6.56 1/s, and the direction is 70 degrees to the right of the depth axis. The velocity at the lower right corner of the model is 30. km/s. I use the local ray-tracing method to compute the attributes of wavefronts in this model. The grid size of the computation is 20 meters. Because the analytical solutions of the wavefronts attributes are known for such a medium, I plot the contours of the wavefront attributes calculated by the local ray-tracing method on the top of the contour plots of the corresponding analytical solutions. Figure  displays the contours of the traveltime and take-off angle fields. The contour intervals are 0.02 second for the traveltime field and 11.4 degrees for the take-off angle field. The contours of the traveltime and take-off angle fields show the trajectories of the wavefronts and rays, respectively. Because of the presence of the velocity gradient, the wavefronts are stretched in the direction of the velocity gradient and the rays are bended in the opposite direction of the velocity gradient. Figure  displays the contours of the fields of curvature radius of wavefront and geometrical spreading factor. The contour intervals are 0.4 km for the curvature radius field and 0.2 km for the geometrical spreading factor field. For a constant velocity model, these two fields are identical. The presence of large velocity gradient makes them quite different from each other. In both Figure  and Figure , the analytical solutions are plotted with white fat lines and the results of the local ray-tracing method are plotted with black thin lines. The near perfect match of two sets of contour lines indicates the high accuracy of the local-ray tracing method.

 

ttmthgra
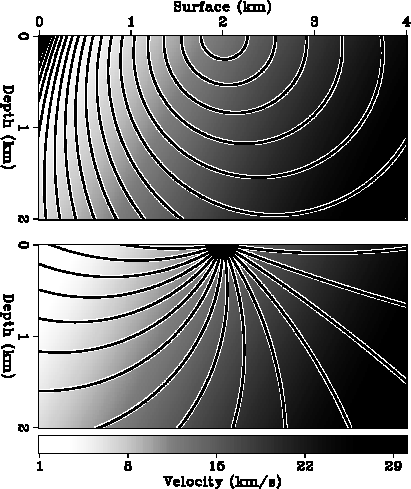
Figure 13 The wavefronts and rays in a linearly varying velocity model. The backgrounds of the two panels show the velocity field. The source is positioned at the top center of the model. The top panel shows the contour lines of the traveltime field with 0.02 second intervals. The bottom panel shows the contour lines of the take-off angle field with 11.4 degree intervals. The white lines shows the analytical solutions and the black lines show the results of the local ray-tracing method.

 

rjjgra
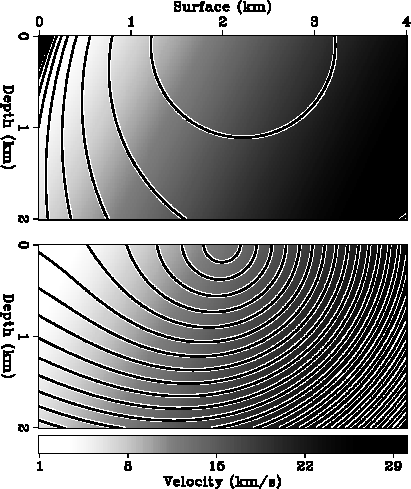
Figure 14 The curvature radii of wavefronts and geometrical spreading factors in a linearly varying velocity model. The backgrounds of the two panels show the velocity field. The source is positioned at the top center of the model. The top panel shows the contour lines of the curvature radius field with 0.4 km intervals. The bottom panel shows the contour lines of the geometrical spreading factor field with 0.2 km intervals. The white lines shows the analytical solutions and the black lines show the results of the local ray-tracing method.

The second synthetic velocity model is a constant velocity field with a 50% negative Gaussian anomaly, and the third one with a 100% positive Gaussian anomaly, as shown in Figure twpn. The size of anomalies is about 200 meters. I use the local ray-tracing method to compute the traveltime field of first arrivals in these models. The grid size used in the computations is 20 meters. In Figure , I compare the results of the traveltime calculations with the wave fields simulated by wave-equation modeling. Because a minimum phase wavelet is used in the wave-equation modeling, the contour lines of the traveltime fields closely follow the first breaks of the wavelets in the corresponding snapshots of the wave fields.

 

twpn
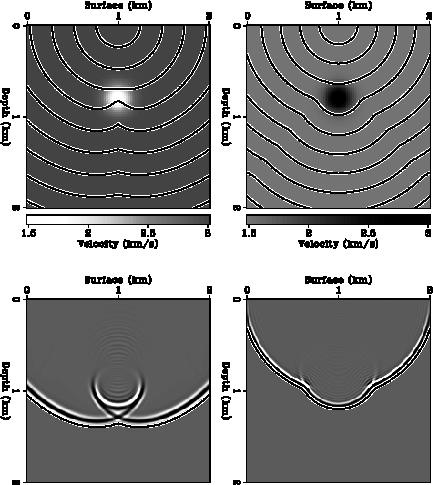
Figure 15 The wavefronts of first arrivals in velocity models with a negative Gaussian anomaly (left) and a positive anomaly (right). The backgrounds of the top panels show the velocity fields. Overlain are the contour lines of the traveltime fields. The contour interval is 0.08 second for the left panel and 0.14 for the right panel. The bottom panel compares the wave fields simulated by wave-equation modeling with the traveltime field calculated by the local ray-tracing method. The intensity plots show snapshots of the wave fields at 0.48 second (left) and 0.7 second (right); the overlain curves are the 0.48s-contour line (left) and 0.7s-contour line (right) of the traveltime fields.