Anelliptic NMO for TI media

Equations () and () relate TI elastic constants and NMO velocities, but to perform and interpret anelliptic moveout we will also need equations relating TI elastic constants and the anelliptic parameter F_W. For the SH wavetype $F_W \equiv 1$,because SH waves in TI media are exactly elliptically anisotropic. For the qP and qSV wavetypes we have to begin by deriving a general form. We proceed by constructing a power series for T(p) in the same form as equation (). That done, we can just match coefficients on like powers of p.

Start with the equation for the traveltime through a layer,  

$$T(\phi_r) = {h \over V_r (\phi_r) \cos (\phi_r) },$$ (30)

where $T(\phi_r)$ is the traveltime through a layer of thickness h, $V_r(\phi_r)$ is the group velocity, and $\phi_{r}$ is the group propagation direction. After some algebra to convert from group to phase variables equation () becomes  

$$T(S) = { h \over \sqrt{W(S)} \sqrt{1-S} \Bigl(1 - S W^{\prime}(S) / W(S) \Bigr)} ,$$ (31)

where T is the group traveltime through a layer of thickness h, S is the square of the sine of the phase propagation direction, W(S) gives the squared phase velocity as a function of S, and $W^\prime$ is the first derivative of W. (See equation () for W(S) in the TI case.)

The ray parameter p can also be expressed as a simple function of S and W(S):  

$$p^2 (S) = { S \over W(S) } .$$ (32)

Expand this equation and equation () to get power series for p²(S) and T(S), respectively.

Finally, we revert p²(S) and composite the resulting series S(p²) with the series T(S), obtaining  

$$T(p) = T(0) \biggl( 1 p^0 + {1 \over 2} W_{x\mbox{\rm\script... ...MO}} + 2 W(0) W^{\prime\prime}(0) \Bigr) p^4 + \ldots \biggr) .$$ (33)

We have used the identity $W(0) + W^{\prime} (0) = W_{x\mbox{\rm\scriptsize NMO}}$(refer back to equation ()) to emphasize the similarity between equations () and (). The term $W(0) W^{\prime\prime}(0)$is also invariant under changes of vertical scale (as we knew it must be from the symmetry of the problem).

Equating the p⁴ terms in equations () and () we obtain the desired equation for the paraxial value of F_W:  

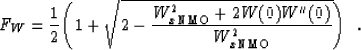$$F_W = {1 \over 2} \Biggl( { 1 + \sqrt{2 - {W^2_{x\mbox{\rm\s... ...e}(0) \over W^2_{x\mbox{\rm\scriptsize NMO}}} } } \Biggr) \ \ .$$ (34)

Although we could substitute equation () into equation () directly, the resulting hash of elastic constants is best avoided. The answer is much simpler in terms of $\delta_{33} = C_{33} - C_{55}$,$\delta_{11} = C_{11} - C_{55}$,and $\chi = C_{13} + C_{55}$.Using these variables, for the TI qP mode we obtain  

$$W^2_{x\mbox{\rm\scriptsize NMO}} + 2 W(0) W^{\prime\prime}(0) =$$ (35)

$$W_{55}^2 + \chi^2 { -3 \chi^2 \delta_{33} + 4 \delta_{11} \d... ...ta_{33} W_{55} + 2 \delta_{33}^2 W_{55} \over \delta_{33}^3 } ,$$

and for the qSV mode  

$$W^2_{x\mbox{\rm\scriptsize NMO}} + 2 W(0) W^{\prime\prime}(0) =$$ (36)

$$W_{55}^2 + (\chi^2 - \delta_{11} \delta_{33}) { \chi^2 \del... ... \chi^2 W_{55} - 2 \delta_{33}^2 W_{55} \over \delta_{33}^3 } .$$

These equations and equation () allow us to find the layer F_W for a given set of TI elastic constants. (Note these equations are not weak-anisotropy approximations.) Unfortunately, given a layer F_W (perhaps found by anelliptic three-term ``velocity'' analysis) these equations do not appear to put simple constraints on the corresponding layer elastic constants.