Marmousi

As an example I used the Marmousi model with its original velocity and density specification. The acoustic modeling was carried out with it (Figures and ). For the elastic modeling I created s-wave velocities assuming a constant Possion's ratio. The elastic modeling results are shown in Figures and . In both cases pressure sources were used and horizontal and vertical displacement components were recorded on the surface.

Figure and compare the divergence of both types of modeling. The divergence is computed from the wave field components identically. It clearly shows that as expected pure acoustic modeling cannot account for mode converted waves. A realistic modeling of the earth should include mode converted waves (p, sv and sh). Since mode conversions are absent in the pure acoustic modeling, the amplitudes are different of even the ``primary'' waves. No energy is leaking into other modes, but stays within the p wave.

 

fig1 Figure 1 Marmousi subsurface velocity model.

 

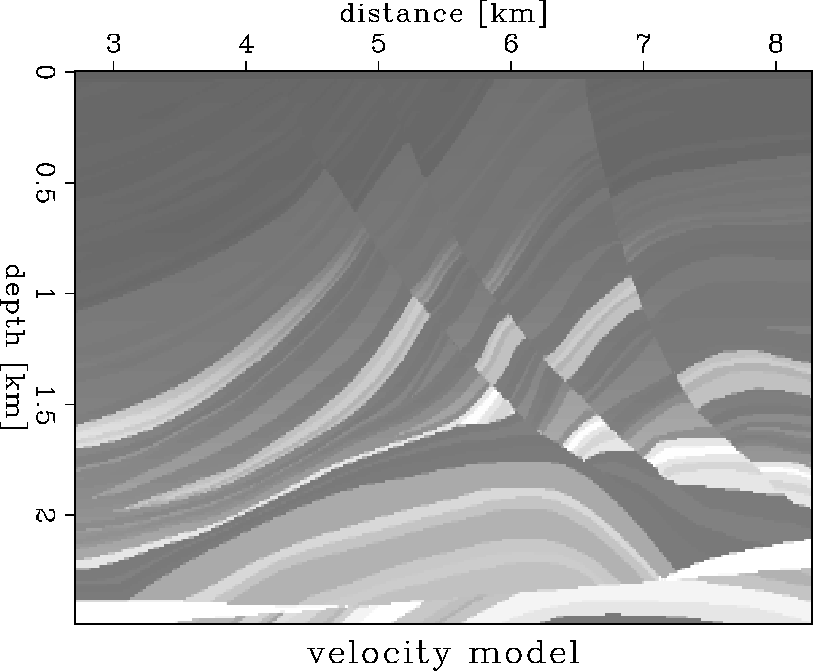fig6 Figure 2 Elastic modeling with a pressure source recorded into a horizontal receiver.

 

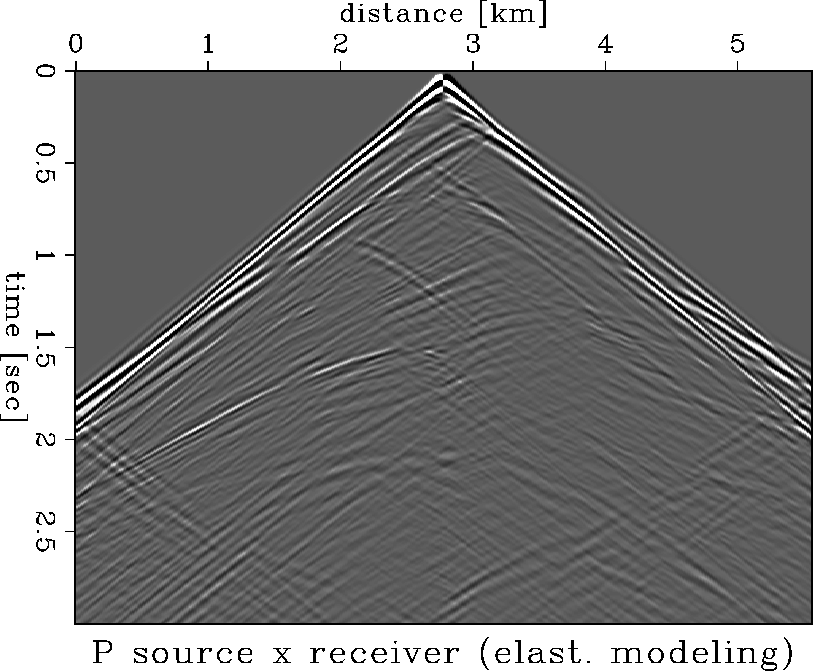fig7 Figure 3 Elastic modeling with a pressure source recorded into a vertical receiver.

 

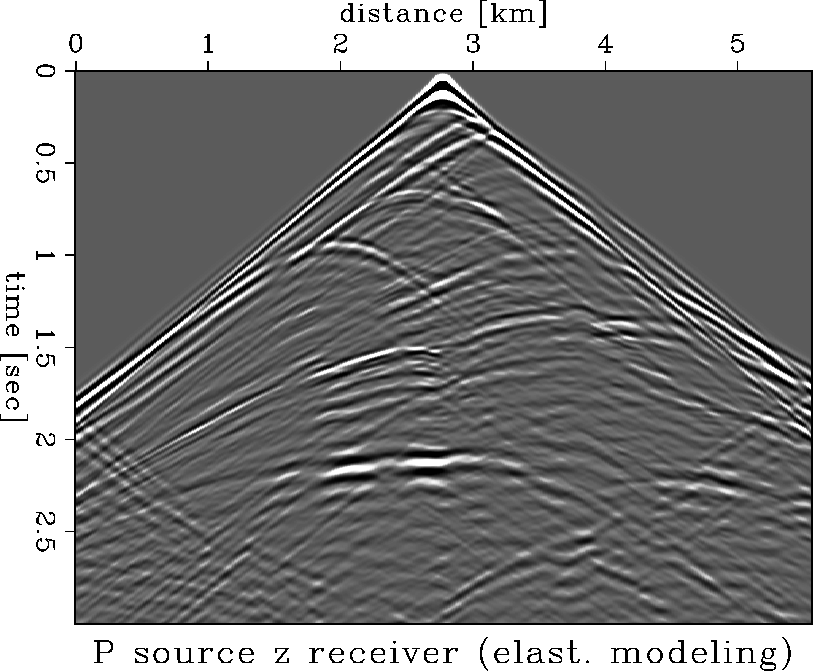fig8 Figure 4 Acoustic modeling with a pressure source recorded into a horizontal receiver.

 

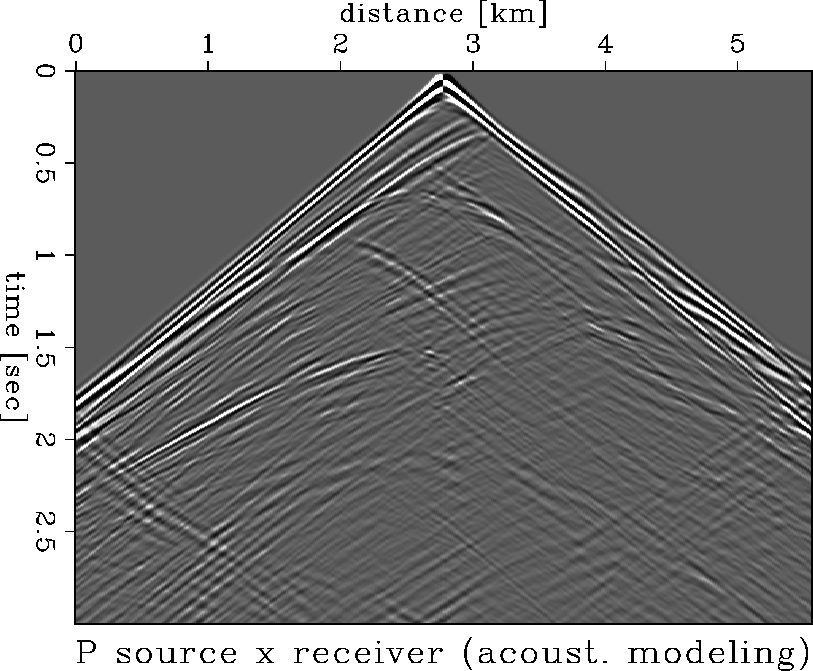fig9 Figure 5 Acoustic modeling with a pressure source recorded into a vertical receiver.

 

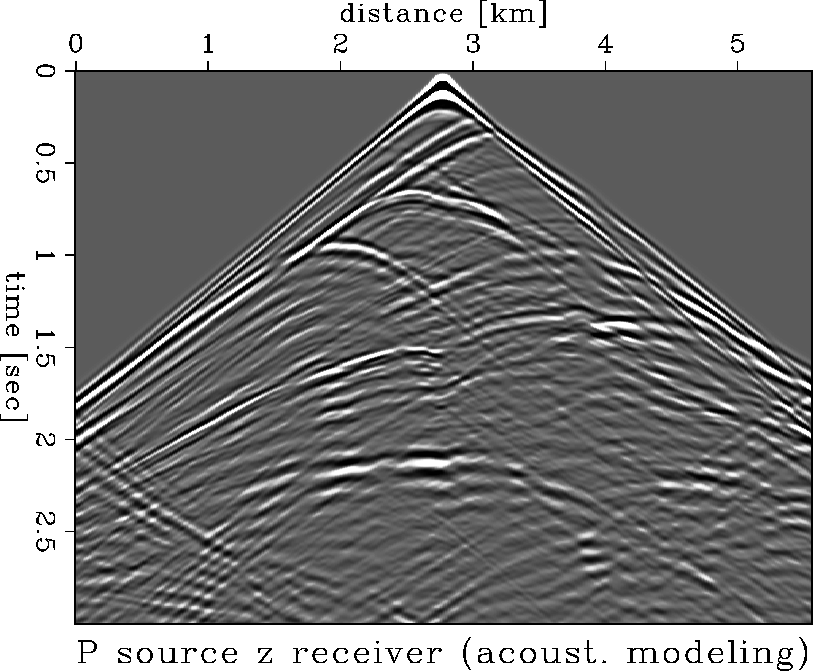fig3 Figure 6 Divergence computed from elastic modeling schemes. There are mode converted waves. Compare it to the acoustic modeling.

 

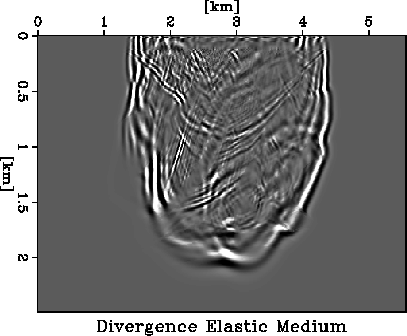fig4 Figure 7 Divergence computed from acoustic modeling schemes. The acoustic modeling does not show mode converted waves.Compare it to the elastic modeling.