LITWEQ method is based on the scalar wave equation for variable velocity media,
| |
(1) |
The basic idea in this method is to rewrite the 2-D scalar
wave equation in a new coordinate system. This allows us to
produce uniformly space grids and to approximate
the solution of (1) by using finite difference.
First, let's define an auxiliary variable
![]() sometimes called pseudo-depth,
sometimes called pseudo-depth,
| (2) |
Second, let's define a reference velocity to measure the lateral velocity variation in the media:
| (3) |
| (4) |
Equation (4) is defined on the
![]() domain which is independent of the velocity.
This is because we have already integrated along it when defining
domain which is independent of the velocity.
This is because we have already integrated along it when defining
![]() in (2). Now, we are ready to
define a linear transformation (independent of the velocity)
that incorporates the solutions of (4) along
their characteristic lines. The linear transformation is:
in (2). Now, we are ready to
define a linear transformation (independent of the velocity)
that incorporates the solutions of (4) along
their characteristic lines. The linear transformation is:
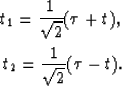 |
(1) | |
| (2) |
Using the chain rule for scalar fields is easy to show the following relations for this particular transformation,
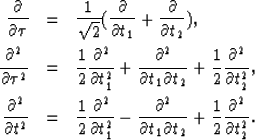 |
(1) | |
| (2) | ||
| (3) |
Finally, using (5) and substituting (6) in (4) we get the LITWEQ operator:
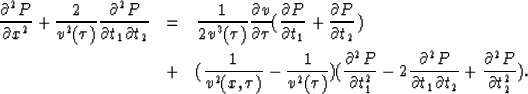 |
||
| (7) |
A detailed derivation of (7) is presented in Li (1986).