Next: Estimating Wij from cross-well
Up: EXAMPLES
Previous: EXAMPLES
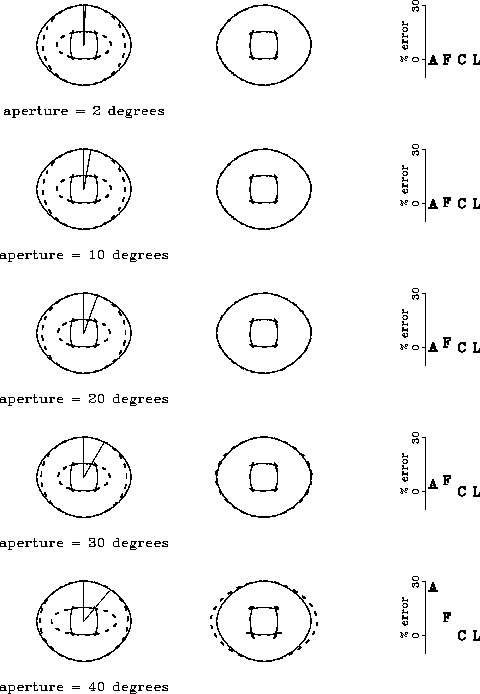
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how the vertical double elliptic
approximation works for different angles around the vertical.
The parameters of the ellipses that approximate
the impulse response have been
calculated at the angles shown by the
straight lines.
The left column compares the given impulse responses for P- and
SV-waves (continuous lines)
with the elliptical approximations around the
vertical (dashed lines). With the four elliptical parameters obtained for
each aperture, I calculate the elastic constants of the medium
by using equation (22). From the estimated elastic
constants, I calculate the corresponding impulse responses for
both P- and SV-waves. The result is shown in the central
column (dashed lines) simultaneously with the
given impulse responses. In most cases (except at 40-degree
aperture) the agreement is excellent. At 40-degree aperture the
horizontal P-wave group velocity has been overestimated and the
shear wave triplication is larger than expected. The right column shows
the absolute value of the percentage error made in the estimation
of the elastic constants. For small angles (
shows how the vertical double elliptic
approximation works for different angles around the vertical.
The parameters of the ellipses that approximate
the impulse response have been
calculated at the angles shown by the
straight lines.
The left column compares the given impulse responses for P- and
SV-waves (continuous lines)
with the elliptical approximations around the
vertical (dashed lines). With the four elliptical parameters obtained for
each aperture, I calculate the elastic constants of the medium
by using equation (22). From the estimated elastic
constants, I calculate the corresponding impulse responses for
both P- and SV-waves. The result is shown in the central
column (dashed lines) simultaneously with the
given impulse responses. In most cases (except at 40-degree
aperture) the agreement is excellent. At 40-degree aperture the
horizontal P-wave group velocity has been overestimated and the
shear wave triplication is larger than expected. The right column shows
the absolute value of the percentage error made in the estimation
of the elastic constants. For small angles (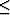 10 degrees), the error
is negligible. For angles between 10 and 30 degrees the error is
smaller in W11 (A) than in W13 (F). At large angles
the error in W11 (A) is the largest, almost 30%.
Notice that up to 30 degrees, even though
the error in the estimation of the elastic constants is not zero but a few
percent, the differences between given and estimated impulse
responses are hard to see.
10 degrees), the error
is negligible. For angles between 10 and 30 degrees the error is
smaller in W11 (A) than in W13 (F). At large angles
the error in W11 (A) is the largest, almost 30%.
Notice that up to 30 degrees, even though
the error in the estimation of the elastic constants is not zero but a few
percent, the differences between given and estimated impulse
responses are hard to see.
vsp
Figure 1 Left: impulse response for P- and SV-waves (continuous lines)
compared with their
elliptical approximations around the vertical (dashed lines). Center:
given impulse responses (continuous) compared to the ones
calculated from the estimated elastic
constants (dashed). Right: absolute value of the error made
in the estimation of the elastic constants when using
the vertical double elliptic approximation.
The elastic constants are A = W11, F = W13,
C = W33, and L = W44. The density is assumed to be unity.

In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the elliptical approximations to the impulse
responses are calculated using two ray angles at a time, one zero
and one nonzero. In
Figure
, the elliptical approximations to the impulse
responses are calculated using two ray angles at a time, one zero
and one nonzero. In
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I show what happens when all these angles
(or different VSP offsets)
are used simultaneously to calculate the elliptical approximations
and the elastic constants. The horizontal P-wave group velocity
is now slightly overestimated and the shear velocities are retrieved well.
The errors in the estimated elastic constants are 6%
in W11 (A) and 4% in W13 (F). The errors
made when using large angles only have been compensated by using also
small angles.
, I show what happens when all these angles
(or different VSP offsets)
are used simultaneously to calculate the elliptical approximations
and the elastic constants. The horizontal P-wave group velocity
is now slightly overestimated and the shear velocities are retrieved well.
The errors in the estimated elastic constants are 6%
in W11 (A) and 4% in W13 (F). The errors
made when using large angles only have been compensated by using also
small angles.
vsp-4angles
Figure 2 Left: impulse response for P- and SV-waves (continuous lines)
compared with their
elliptical approximations around the vertical (dashed lines).
All ray angles shown are used simultaneously to
calculate the elliptical approximations. Center:
given impulse responses (continuous) compared to the ones
calculated from the estimated elastic
constants (dashed). Right: absolute value of the error made
in the estimation of the elastic constants when using
the vertical double elliptic approximation.
The elastic constants are A = W11, F = W13,
C = W33, and L = W44.






Next: Estimating Wij from cross-well
Up: EXAMPLES
Previous: EXAMPLES
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how the vertical double elliptic
approximation works for different angles around the vertical.
The parameters of the ellipses that approximate
the impulse response have been
calculated at the angles shown by the
straight lines.
The left column compares the given impulse responses for P- and
SV-waves (continuous lines)
with the elliptical approximations around the
vertical (dashed lines). With the four elliptical parameters obtained for
each aperture, I calculate the elastic constants of the medium
by using equation (22). From the estimated elastic
constants, I calculate the corresponding impulse responses for
both P- and SV-waves. The result is shown in the central
column (dashed lines) simultaneously with the
given impulse responses. In most cases (except at 40-degree
aperture) the agreement is excellent. At 40-degree aperture the
horizontal P-wave group velocity has been overestimated and the
shear wave triplication is larger than expected. The right column shows
the absolute value of the percentage error made in the estimation
of the elastic constants. For small angles (
shows how the vertical double elliptic
approximation works for different angles around the vertical.
The parameters of the ellipses that approximate
the impulse response have been
calculated at the angles shown by the
straight lines.
The left column compares the given impulse responses for P- and
SV-waves (continuous lines)
with the elliptical approximations around the
vertical (dashed lines). With the four elliptical parameters obtained for
each aperture, I calculate the elastic constants of the medium
by using equation (22). From the estimated elastic
constants, I calculate the corresponding impulse responses for
both P- and SV-waves. The result is shown in the central
column (dashed lines) simultaneously with the
given impulse responses. In most cases (except at 40-degree
aperture) the agreement is excellent. At 40-degree aperture the
horizontal P-wave group velocity has been overestimated and the
shear wave triplication is larger than expected. The right column shows
the absolute value of the percentage error made in the estimation
of the elastic constants. For small angles (