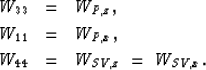
To estimate W11, W33, W44, and W13 directly from equation (1a), we need at least four phase velocities at four different angles between 0 and 90 degrees. Wij is the solution of a system of nonlinear equations where the independent term is formed by these phase velocities. Along the axes, the system of equations is almost diagonal and the estimation of three elastic constants (W33, W11, and W44) is straightforward:
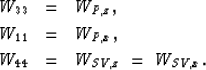 |
(1) | |
| (2) | ||
| (3) |
This approach, although simple in theory, is not applicable in many practical situations because wide aperture data are required (the angles of the observations must include 0, 90 degrees, and one intermediate measurement) in order to simplify the system of equations. This is not the case for most single-geometry data sets (either surface, or cross-well or VSP) where no rays travel along (at least) one of the axes and therefore, phase velocities along both axes cannot be estimated without having to assume a velocity symmetry (e.g., isotropic, elliptical, TI).