




Next: TRANSMISSIVITY SIMULATION
Up: MODELING LAYERS
Previous: MODELING LAYERS
To construct a Markov chain, all we need
to know are the probability for each state (M-1 parameters) and the
blockiness of the sequence(the single remaining parameter).
In case of M = 2, telegraph matrix can be made from those parameters
as follows.
| 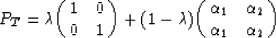 |
(1) |
where 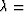 blockiness,
blockiness,
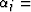 the probability of state j.
The blockiness
the probability of state j.
The blockiness 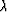 is obtained from the exponential coefficient
of well logs' correlation data. The left term of the right hand side
describes the tendency to remain in the same state as before, and
the right one is for the tendency to change into another state.
Markov chains depend only on the last state. Once the current state
is determined, it forgets all the previous states and choose the
next state only from the current information.
If the first state is state 1, the probability state
vector
is obtained from the exponential coefficient
of well logs' correlation data. The left term of the right hand side
describes the tendency to remain in the same state as before, and
the right one is for the tendency to change into another state.
Markov chains depend only on the last state. Once the current state
is determined, it forgets all the previous states and choose the
next state only from the current information.
If the first state is state 1, the probability state
vector 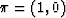 . The probability for the continuous state
. The probability for the continuous state
 becomes
becomes
| 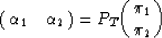 |
(2) |
After obtaining  , a random number (from 0 to 1)
is used to choose new
state and we get the new
, a random number (from 0 to 1)
is used to choose new
state and we get the new  for the next lottery.
for the next lottery.





Next: TRANSMISSIVITY SIMULATION
Up: MODELING LAYERS
Previous: MODELING LAYERS
Stanford Exploration Project
11/17/1997