AGREEMENT WITH THE EQUATIONS IN TWO DIMENSIONS

The 2-D system derived by Artley 1992 is a set of four equations with four unknowns. It can be retrieved by replacing the vectorial ray parameters with their scalar form (since the vectors are now in a common plane). The first relation of system (14) then becomes  

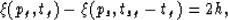$$\xi(p_g,t_g) - \xi(p_s,t_{sg}-t_g) = 2h ,$$ (18)

where h is the half offset. The fourth relation becomes  

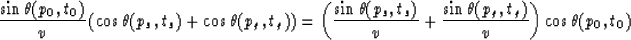$$\frac{\sin \theta(p_0,t_0)}{v} \left( \cos \theta(p_s,t_s) ... ... + \frac{\sin \theta(p_g,t_g)}{v} \right) \cos \theta(p_0,t_0)$$ (19)

and can be simplified to  

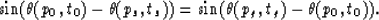$$\sin( \theta(p_0,t_0) - \theta(p_s,t_s) ) = \sin( \theta(p_g,t_g) - \theta(p_0,t_0) ) .$$ (20)

Finally, we obtain the bisection condition as shown by Artley 1992, as follows:  

$$\theta(p_0,t_0) = \frac{1}{2}\left[ \theta(p_s,t_s) + \theta(p_g,t_g) \right] .$$ (21)