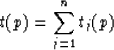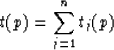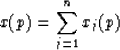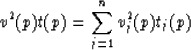Layered impedance

As a start, it is convenient also to limit impedance to a layered model, and to impose axisymmetry on the velocity functions. Conventional first-pass velocity analysis often makes a like assumption.

The surface kinematics of reflection wavefronts in such a (not necessarily isotropic) layered earth may be exactly and completely described by two functions of the ray parameter, p. These are the travel-time function, t(p), and the offset function, x(p). The kinematics of a set of such layers is simply and exactly formed because these functions are elements of Abelian groups. That is, the reflection response from the base of n such layers arranged in any order is given by

$$t(p) = \sum_{j=1}^{n}t_{j}(p)$$

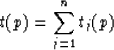
and

$$x(p) = \sum_{j=1}^{n}x_{j}(p)$$

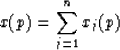
If we now define v²(p) = x(p)/pt(p) then v²(p)t(p) = x(p)/p. But this latter is addable for constant p and so then must be v²(p)t(p). That is,

$$v^{2}(p)t(p) = \sum_{j=1}^{n}v_{j}^{2}(p)t_{j}(p)$$

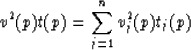
where v(p) is some as yet unspecified velocity.