TIMING ON THE CM5

Both the slow Fourier transform (SFT) and interpolation algorithms have been implemented on the CM5 and their running times compared. The SFT involves a matrix multiplication and therefore is an algorithm in $N \times N$. However, a parallel machine with P processors will perform these computations in a time proportional to $N \times N / P$with some additional but smaller communication cost.

The serial implementation of the interpolation filter requires a number of computations proportional to $N \times m$, where m is the length of the filters. For large values of N, the interpolation algorithm will prove more efficient than the SFT algorithm. However, because the SFT algorithm runs P times faster on a parallel machine whereas the interpolation algorithm does not improve its speed, what was considered a large number N appears now as a smaller number. Indeed, for a trace length of 2048, the SFT algorithm runs four times as fast as the other:

SFT:                111.7 real       100.2 user         0.7 sys
Interpolation:      489.0 real       471.8 user         4.5 sys

Moreover, as the trace length decreases, the running time ratio increases in such a way that, for 1024 time samples (a usual trace length), it becomes one to eight:

SFT:                 99.7 real        30.0 user         1.7 sys
Interpolation:      447.8 real       241.0 user         6.0 sys

The user times are more significant than the real times which depend a lot on the current load of the machine.

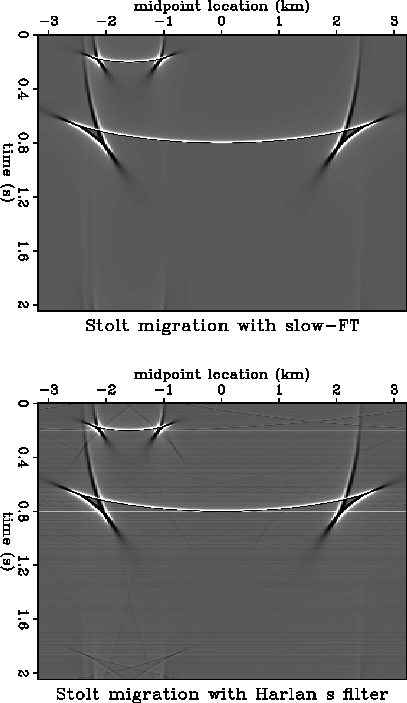
The slow Fourier transform algorithm proves efficient not only for its speed but also for the artifact-free migration that it produces. Figure  illustrates this point.

 

compare
Figure 1 Both figures are impulse responses of Stolt migration. The top figure was obtained with the algorithm involving the slow Fourier transform step. The bottom figure was obtained with the algorithm applying Harlan's 10-point filter in the frequency-wave-number domain. Harlan's filter removes only a part of the artifacts caused by frequency interpolation, whereas the slow Fourier transform algorithm yields a clean image. In both cases, a three-point filter (1,2,1) removes the Nyquist noise inherent to the frequency limitation of the discrete Fourier domain in both t and x. Click on the following button to see a movie alternating the two pictures.