Ideal weighting functions for stacking

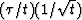The difference between stacking as defined by nmo0() and by nmo1() is in the weighting function $(\tau/t)(1/\sqrt{t})$.Notice that 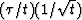$(\tau/t)(1/\sqrt{t})$can be factored into two weights, $\tau$ and t^-3/2. One weight could be applied before NMO and the other after. That would also be more efficient than weighting inside NMO, as does nmo1(). Additionally, it is likely that these weighting functions should take into account data truncation at the cable's end. Stacking is the most important operator in seismology. Perhaps some objective measure of quality can be defined and arbitrary powers of t, x, and $\tau$can be adjusted until the optimum stack is defined. Likewise, we should consider weighting functions in the spectral domain. As the weights $\tau$ and t^-3/2 tend to cancel one another, perhaps we should filter with opposing filters before and after NMO and stack.

The preconditioners used here are related to wave theory in a constant velocity earth. We can expect improvement if we redesign them for a stratified earth. I expect the familiar velocity dependent divergence correction would appear.