




Next: OPTIMIZATION
Up: Harlan: Flexible tomography
Previous: PARAMETERIZATION OF PATHS
Here I show that traveltime data are easily linearized
as a function of the parameters describing the velocity
basis functions.
The functional form of an anisotropic group velocity must
depend on the location and on the direction of a raypath.
The vector 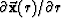 points
tangent to a given point on a raypath.
Since
points
tangent to a given point on a raypath.
Since 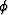 is the angle of a raypath from the vertical axis
of symmetry
is the angle of a raypath from the vertical axis
of symmetry 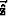 , we can calculate
the angle in the group velocity (4) as
a function of the position along the raypath:
, we can calculate
the angle in the group velocity (4) as
a function of the position along the raypath:
| 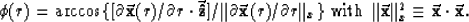 |
(8) |
For this reason, we can write the parameterized group velocity
![$V [ \vec{ \bf x}(r) , \phi ]$](img33.gif) in (4)
as a function of the location and a tangent vector (with arbitrary magnitude).
in (4)
as a function of the location and a tangent vector (with arbitrary magnitude).
A given raypath 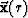 , for r from 0 to 1, integrates
for the traveltime
, for r from 0 to 1, integrates
for the traveltime
| ![\begin{displaymath}
t = \int_0^1 V [ \vec{ \bf x}(r) , \phi(r) ]^{-1}
\Vert \partial \vec{ \bf x}(r) / \partial r \Vert _x dr .\end{displaymath}](img34.gif) |
(9) |
Because the raypath represents a stationary minimum, tomography recognizes
that perturbation of a valid raypath affects
traveltime only to second order. To perturb traveltimes linearly
with finite perturbations of slowness along a path, we need only
integrate the slowness perturbations along the original path:
| 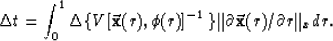 |
(10) |
The perturbation of slowness is given by
the parameterization in (5).
This formulation provides the linearized perturbation
of the traveltime data as a function of perturbed velocity parameters.
The adjoint uses the same weights
for a backprojection of traveltime perturbations upon the
velocity parameters.





Next: OPTIMIZATION
Up: Harlan: Flexible tomography
Previous: PARAMETERIZATION OF PATHS
Stanford Exploration Project
11/12/1997
![]() points
tangent to a given point on a raypath.
Since
points
tangent to a given point on a raypath.
Since ![]() is the angle of a raypath from the vertical axis
of symmetry
is the angle of a raypath from the vertical axis
of symmetry ![]() , we can calculate
the angle in the group velocity (4) as
a function of the position along the raypath:
, we can calculate
the angle in the group velocity (4) as
a function of the position along the raypath:
![]() , for r from 0 to 1, integrates
for the traveltime
, for r from 0 to 1, integrates
for the traveltime