| (2) |
For small residuals R, the Huber function reduces to the usual L2 least squares penalty function, and for large R it reduces to the usual robust (noise insensitive) L1 penalty function. Notice the continuity at |R|= h where the Huber function switches from its L2 range to its L1 range. Likewise derivatives are continuous at the junctions |R|=h:
| (3) |
The derivative of the Huber function
is what we commonly call the clip function ![]() .
.
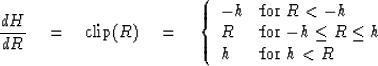 |
(4) |
Now let us set out to minimize a sum
of Huber functions of all the components of the residual
![]() where the residual
where the residual ![]() is perturbed by the addition
of a small amount of gradient
is perturbed by the addition
of a small amount of gradient ![]() and previous step
and previous step ![]() .The perturbed residual is
.The perturbed residual is
![]() where we are given
where we are given
![]() ,
,![]() ,
,![]() , and
we seek to find
, and
we seek to find ![]() and
and ![]() by setting to zero derivatives of
by setting to zero derivatives of ![]() by
by ![]() and
and ![]() .For simplicity we assume that
.For simplicity we assume that ![]() and
and ![]() are small
and that we do not need to worry about components jumping between
the L2 and L1 range portions of the Huber function.
Obviously residual component values will often jump between the two ranges,
and because of that, we must iterate the steps I define next:
are small
and that we do not need to worry about components jumping between
the L2 and L1 range portions of the Huber function.
Obviously residual component values will often jump between the two ranges,
and because of that, we must iterate the steps I define next:
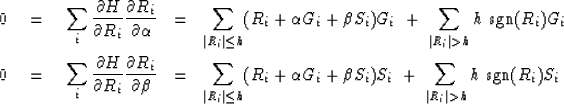 |
(5) | |
| (6) |
![\begin{eqnarray}
\left\{
\sum_{\vert R_i\vert\le h}
\left[
\begin{array}
{cc}
...
...i \ {\rm clip}(R_i)
\\ S_i \ {\rm clip}(R_i)
\end{array}\right]\end{eqnarray}](img18.gif) |
(7) | |
| (8) |
From the economical viewpoint,
whether or not we would
iterate for the values of ![]() and
and ![]() would depend on whether
it was
costly to compute
the new gradient
would depend on whether
it was
costly to compute
the new gradient
![]() ,that is, whether
,that is, whether
![]() and
and ![]() are costly to apply.
If they are, we would want to make sure we got the
most value from each
are costly to apply.
If they are, we would want to make sure we got the
most value from each ![]() we had,
so we would iterate the plane search for
we had,
so we would iterate the plane search for ![]() .Otherwise, if it was cheap to compute the next gradient
.Otherwise, if it was cheap to compute the next gradient
![]() ,we would do so rather than making the best possible use
of the existing gradient (by repeated plane search).
,we would do so rather than making the best possible use
of the existing gradient (by repeated plane search).
The economical viewpoint may be surpassed by
the need to avoid trouble.
Limited experiences so far show that
instabilities can arise
going from one ![]() to the next.
We should be able to control them by
iterating to convergence for each
to the next.
We should be able to control them by
iterating to convergence for each ![]() .Failing in that,
I believe theory says we are assured stable
convergence if we drop back from
conjugate directions to steepest descent.
All these extra precautions
will require more than the straightforward coding below.
.Failing in that,
I believe theory says we are assured stable
convergence if we drop back from
conjugate directions to steepest descent.
All these extra precautions
will require more than the straightforward coding below.